
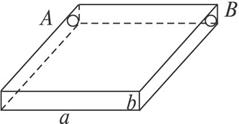
思路分析:题意中的“杂质的质量分数”可按“杂质的含量”理解,设为y,由题意y与ab成反比,又设比例系数为k,则y=![]() .又由于受箱体材料多少的限制,a,b之间应有一定的关系式,即2×(2b)+2ab+2a=60,因此该题的数学模型是:已知ab+a+2b=30,a>0,b>0,当y=
.又由于受箱体材料多少的限制,a,b之间应有一定的关系式,即2×(2b)+2ab+2a=60,因此该题的数学模型是:已知ab+a+2b=30,a>0,b>0,当y=![]() 最小时,求a,b的值.
最小时,求a,b的值.
解法一:设流出的水中杂质的质量分数为y,由题意
y=![]() (k>0),其中k为比例系数.
(k>0),其中k为比例系数.
又据题意设2×2b+2ab+2a=60(a>0,b>0),
∴b=![]() (由a>0,b>0,可得a<30).
(由a>0,b>0,可得a<30).
∴y=![]() =
=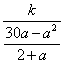 .
.
令t=a+2,则a=t-2,
从而![]()
=![]() ≤34-
≤34-![]()
![]() =18,
=18,
∴y=![]() ≥
≥![]() .
.
当且仅当t=64t,即t=8,
∴a=6时取“=”号.
由a=6,得b=3.
综上所述,当a=6 m,b=3 m时,经沉淀后流出的水中杂质的质量分数最小.
解法二:设流出的水中杂质的质量分数为y,依题意y=![]() ,其中k为比例系数,k>0,要求y的最小值,必须求解ab的最大值.
,其中k为比例系数,k>0,要求y的最小值,必须求解ab的最大值.
题设4b+2ab+2a=60,即ab+2b+a=30(a>0,b>0),
∵a+2b≥![]() (当且仅当a=2b时取“=”号),
(当且仅当a=2b时取“=”号),
∴ab+![]()
![]() ≤30,可解得0<ab≤18.
≤30,可解得0<ab≤18.
由a=2b,及ab+a+2b=30,可得a=6,b=3.
即a=6,b=3时,ab取最大值,从而y值最小.


科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
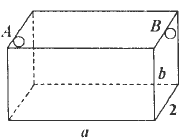
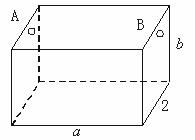
如下图,为处理含有某种杂质的污水,要制造一底宽为2m的无盖长方体沉淀箱.污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为am,高度为bm.已知流水中含杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60m2,问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量最小?(A、B两孔的面积忽略不计)?
查看答案和解析>>
科目:高中数学 来源:导学大课堂选修数学1-1苏教版 苏教版 题型:044
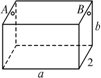
如下图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a、b的乘积成反比.现有制箱材料60平方米,问当a、b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com