练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数，．

       （1）当时，若上单调递减，求a的取值范围；

       （2）求满足下列条件的所有整数对：存在，使得的最大值， 的最小值；

    （1）当时，，     ………………………………………1分

           若，，则在上单调递减，符合题意；………3分

           若，要使在上单调递减，

           必须满足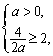 ………………………………#k#s5u……………………5分

           ∴．综上所述，a的取值范围是   …………………………………6分

           （2）若，，则无最大值， 故，∴为二次函数，       

           要使有最大值，必须满足

    即且，             …………………………………………8分

           此时，时，有最大值．  ………………………………………9分

           又取最小值时，，  ………………………………………………………10分

           依题意，有，则，  …………11分

           ∵且，∴，得，   ………………12分

           此时或．

           ∴满足条件的整数对是．         ……………………………13分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    		x
    -1    ，则f（x）的最小值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•自贡一模）已知函数f(x)=  
    x+1
    ，  x
    ≤0，
    log2x
    ，x＞0
    ，
    则函数y=f[f（x）]+1的零点个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（2x+1）的定义域为[1，2]，则函数f（4x+1）的定义域为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•永州一模）已知函数f(x)=ln(1+x)-p
    		x
    ．
    （1）若函数f（x）在定义域内为减函数，求实数p的取值范围；
    （2）如果数列{an}满足a1=3，an+1=[1+
    1
    n2(n+1)2
    ]an+
    1
    4n
    ，试证明：当n≥2时，4≤an＜4e
    3
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•浦东新区一模）已知函数f(x)=
    		x2+1
    -ax    ，其中a＞0．
    （1）若2f（1）=f（-1），求a的值；
    （2）当a≥1时，判断函数f（x）在区间[0，+∞）上的单调性；
    （3）若函数f（x）在区间[1，+∞）上是增函数，求a的取值范围．

    查看答案和解析>>

    同步练习册答案