已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*).将集合{x|x=an,n∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,…
(1)写出c1,c2,c3,c4;
(2)求证:在数列{cn}中,但不在数列{bn}中的项恰为a2,a4,…,a2n,…;
(3)求数列{cn}的通项公式.
解:(1)a
1=3×1+6=9; a
2=3×2+6=12 a
3=3×3+6=15
b
1=2×1+7=9 b
2=2×2+7=11 b
3=2×3+7=13
∴c
1=9;c
2=11;c
3=12;c
4=13
(2)解对于a
n=3n+6,
当n为奇数时,设为n=2k+1
则3n+6=2(3k+1)+7∈{b
n}
当n为偶数时,设n=2k则3n+6=6k-1+7不属于{b
n}
∴在数列{c
n}中,但不在数列{b
n}中的项恰为a
2,a
4,…,a
2n,…;
(3)b
3k-2=2(3k-2)+7=a
2k-1b
3k-1=6k+5
a
2k=6k+6
b
3k=6k+7
∵6k+3<6k+5<6k+6<6k+7
∴当k=1时,依次有b
1=a
1=c
1,b
2=c
2,a
2=c
3,b
3=c
4…
∴
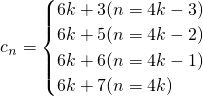
分析:(1)利用两个数列的通项公式求出前3项,按从小到大挑出4项.
(2)对于数列{a
n},对n从奇数与偶数进行分类讨论,判断是否能写成2n+7的形式.
(3)对{a
n}中的n从从奇数与偶数进行分类讨论,对{b
n}中的n从被3除的情况分类讨论,判断项的大小,求出数列的通项.
点评:本题考查利用数列的通项公式求数列的项、考查判断某项是否属于一个数列是看它是否能写出通项形式、考查分类讨论的数学数学方法.

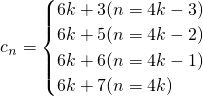


 阅读快车系列答案
阅读快车系列答案