
已知函数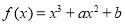 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线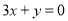 平行.
平行.
(1)求函数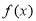 的解析式;
的解析式;
(2)求函数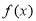 在区间[0,t](0<t<3)上的最大值和最小值;
在区间[0,t](0<t<3)上的最大值和最小值;
(3)在(1)的结论下,关于x的方程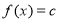 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
(1)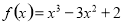 (2)答案见解析 (3)
(2)答案见解析 (3)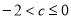
【解析】
试题分析:(1)由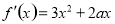 及曲线在
及曲线在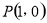 处的切线斜率为
处的切线斜率为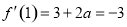 ,即可求得
,即可求得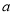 ,又函数过
,又函数过 点,即可求的
点,即可求的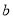 .
.
(2)由(1)易知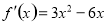 ,令
,令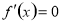 可得
可得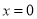 或
或 ,然后对
,然后对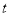 进行分类讨论,确定函数
进行分类讨论,确定函数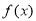 在
在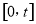 的单调性,即可求出函数
的单调性,即可求出函数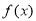 在
在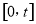
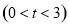 上的最大值和最小值;
上的最大值和最小值;
(3)构造函数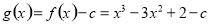 ,研究函数
,研究函数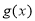 的单调性,列出该方程有两个相异的实根的不等式组,求出实数
的单调性,列出该方程有两个相异的实根的不等式组,求出实数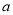 的取值范围.
的取值范围.
试题解析:(1)因为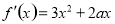 ,曲线在
,曲线在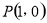 处的切线斜率为
处的切线斜率为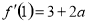 ,即
,即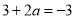 ,所以
,所以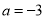 .
.
又函数过 点,即
点,即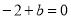 ,所以
,所以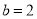 .
.
所以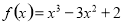 .
.
(2)由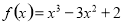 ,
,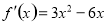 .
.
由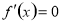 ,得
,得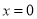 或
或 .
.
①当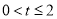 时,在区间
时,在区间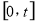 上
上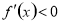 ,
,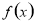 在
在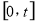 上是减函数,
上是减函数,
所以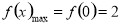 ,
,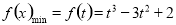 .
.
②当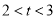 时,当
时,当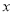 变化时,
变化时,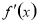 、
、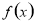 的变化情况见下表:
的变化情况见下表:
| 0 |
| 2 |
|
|
| 0 | - | 0 | + | + |
| 2 |
| -2 | ? |
|
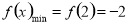 ,
,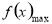 为
为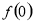 与
与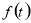 中较大的一个.
中较大的一个.
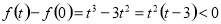 .
.
所以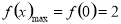 .
.
(3)令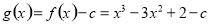 ,
,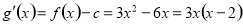 .
.
在 上,
上,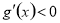 ;在
;在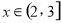 上,
上,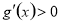 .要使
.要使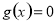 在
在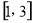 上恰有两个相异的实根,则
上恰有两个相异的实根,则
 解得
解得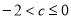 .
.
考点:利用导数求函数的最值;利用导数求参数的范围.


科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使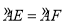 .
.
(1)求证:E、D、G、O四点共圆;
(2)如果CB=OB,试求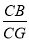 的值.
的值.

查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
某汽车销售公司在A、B两地销售同一种品牌的汽车,在A地的销售利润(单位:万元)为y1=4.1x-0.1x2,在B地的销售利润(单位:万元)为y2=2x,其中x为销售量(单位:辆).若该公司在两地共销售16辆这种品牌汽车,则能获得的最大利润是( )
A.10.5万元 B.11万元 C.43万元 D.43.025万元
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:填空题
古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···,第n个三角形数为 。记第n个k边形数为N(n,k)(
。记第n个k边形数为N(n,k)(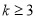 ),以下列出了部分k边形数中第n个数的表达式:
),以下列出了部分k边形数中第n个数的表达式:
三角形数 N(n,3)=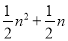
正方形数 N(n,4)=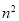
五边形数 N(n,5)=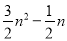
六边形数 N(n,6)=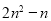
可以推测N(n,k)的表达式,由此计算N(10,24)= ____________
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:选择题
口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若P(X=2)=,则n的值为( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
设椭圆C: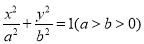 的离心率
的离心率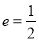 ,右焦点到直线
,右焦点到直线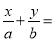 1的距离
1的距离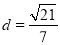 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)过点O作两条互相垂直的射线,与椭圆C分别交于A、B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com