
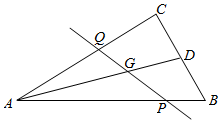
 如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$]. 分析 易知存在m,使$\overrightarrow{AG}$=m$\overrightarrow{AQ}$+(1-m)$\overrightarrow{AP}$,且$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$(y$\overrightarrow{AQ}$+x$\overrightarrow{AP}$),从而可得x+y=3,且1≤x≤2,从而化为二次函数求范围.
解答 解:∵P,G,Q三点共线,
∴存在m,使$\overrightarrow{AG}$=m$\overrightarrow{AQ}$+(1-m)$\overrightarrow{AP}$,
又∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$(y$\overrightarrow{AQ}$+x$\overrightarrow{AP}$),
∴$\frac{1}{3}$(y$\overrightarrow{AQ}$+x$\overrightarrow{AP}$)=m$\overrightarrow{AQ}$+(1-m)$\overrightarrow{AP}$,
∴x+y=3,
又∵$\overrightarrow{AB}$=x$\overrightarrow{AP}$,
∴1≤x≤2,
故xy=x(3-x)=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
故2≤-(x-$\frac{3}{2}$)2+$\frac{9}{4}$≤$\frac{9}{4}$,
故答案为:[2,$\frac{9}{4}$].
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用,同时考查了二次函数的性质应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,0] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-2,2] | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -2 | C. | 1 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
| PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com