
分析 由(1+x-2x2)5=[1+x(1-2x)]5,利用二项式展开式的通项公式,即可求出(1+x-2x2)5的展开式中x4项的系数.
解答 解:因为(1+x-2x2)5=[1+x(1-2x)]5,
其展开式的通项公式为:
Tr+1=${C}_{5}^{r}$•[x(1-2x)]r=${C}_{5}^{r}$•xr•[$\sum_{k=0}^{r}$${C}_{r}^{k}$•(-2x)k]=${C}_{5}^{r}$•[$\sum_{k=0}^{r}$${C}_{r}^{k}$•(-2)k•xk+r];
令k+r=4,且0≤r≤5,0≤k≤r,k、r∈N,
则$\left\{\begin{array}{l}{r=4}\\{k=0}\end{array}\right.$,或$\left\{\begin{array}{l}{r=3}\\{k=1}\end{array}\right.$,或$\left\{\begin{array}{l}{r=2}\\{k=2}\end{array}\right.$;
所以(1+x-2x2)5的展开式中x4项的系数为:
${C}_{5}^{4}$•${C}_{4}^{0}$+${C}_{5}^{3}$•${C}_{3}^{1}$•(-2)+${C}_{5}^{2}$•${C}_{2}^{2}$•(-2)2=-15.
故答案为:-15.
点评 本题考查了二项式展开式定理的应用问题,解题时应用展开式的通项公式求特定项的系数,是基础题目.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{3}$ | B. | $-2-\sqrt{3}$ | C. | $-2+\sqrt{3}$ | D. | $2+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$$\overrightarrow a$+$\frac{1}{3}$$\overrightarrow b$ | B. | $\frac{1}{3}$$\overrightarrow a$+$\frac{2}{3}$$\overrightarrow b$ | C. | $\frac{3}{5}$$\overrightarrow a$+$\frac{4}{5}$$\overrightarrow b$ | D. | $\frac{4}{5}$$\overrightarrow a$+$\frac{3}{5}$$\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
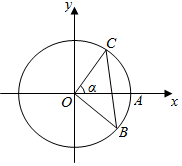 如图,⊙O与x轴的正半轴的交点为A,点C、B在⊙O上,且点C位于第一象限,点B的坐标为($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α(α为锐角).
如图,⊙O与x轴的正半轴的交点为A,点C、B在⊙O上,且点C位于第一象限,点B的坐标为($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α(α为锐角).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com