
【题目】(1)有物理、化学、生物三个学科竞赛各设冠军一名,现有![]() 人参赛可报任意学科并且所报学科数不限,则最终决出冠军的结果共有多少种可能?
人参赛可报任意学科并且所报学科数不限,则最终决出冠军的结果共有多少种可能?
(2)有![]() 共
共![]() 个数,从中取
个数,从中取![]() 个数排成一个五位数,要求奇数位上只能是奇数,则共可排成多少个五位数?
个数排成一个五位数,要求奇数位上只能是奇数,则共可排成多少个五位数?
(3)有![]() 共
共![]() 个数,从中取
个数,从中取![]() 个数排成一个五位数,要求奇数只在奇数位上,则共可排成多少个五位数?
个数排成一个五位数,要求奇数只在奇数位上,则共可排成多少个五位数?
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,椭圆
两点,椭圆![]() 的右顶点为
的右顶点为![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,且定点
,且定点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图象大致是( )
的部分图象大致是( )
A.  B.
B. 
C.  D.
D. 
【答案】D
【解析】当![]() 时,
时, ![]() ,所以去掉A,B;
,所以去掉A,B;
因为![]() ,所以
,所以![]() ,因此去掉C,选D.
,因此去掉C,选D.
点睛:有关函数图象识别问题的常见题型及解题思路(1)由解析式确定函数图象的判断技巧:(1)由函数的定义域,判断图象左右的位置,由函数的值域,判断图象的上下位置;②由函数的单调性,判断图象的变化趋势;③由函数的奇偶性,判断图象的对称性;④由函数的周期性,判断图象的循环往复.(2)由实际情景探究函数图象.关键是将问题转化为熟悉的数学问题求解,要注意实际问题中的定义域问题.
【题型】单选题
【结束】
8
【题目】《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三个内角
三个内角![]() 所对的边分别是
所对的边分别是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圆半径为2,求
的外接圆半径为2,求![]() 周长的最大值.
周长的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由正弦定理将边角关系化为边的关系![]() ,再根据余弦定理求角
,再根据余弦定理求角![]() ,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
试题解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因为![]() ,则
,则![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周长![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴当![]() 即
即![]() 时
时![]()
∴当![]() 时,
时, ![]() 周长的最大值为
周长的最大值为![]() .
.
【题型】解答题
【结束】
18
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中:  ,
, ![]() ,
, ![]()

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() .
.
(1)证明: ![]() ;
;
(2)若当![]() 时,
时, 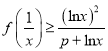 ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据切线过点
,再根据切线过点![]() ,解得
,解得![]() 导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为
导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为![]() ,分离得
,分离得![]() ,再利用导数求函数
,再利用导数求函数![]() 单调性,利用罗伯特法则求最大值,即得
单调性,利用罗伯特法则求最大值,即得![]() 的取值范围.
的取值范围.
试题解析:(1)曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,即
,即![]()
由题意得![]() ,解得
,解得![]()
所以![]()
从而![]()
因为当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在区间
在区间![]() 上是减函数,区间
上是减函数,区间![]() 上是增函数,
上是增函数,
从而![]() .
.
(2)由题意知,当![]() 时,
时, ![]() ,所以
,所以![]()
从而当![]() 时,
时, ![]() ,
,
由题意知 ,即
,即![]() ,其中
,其中![]()
设![]() ,其中
,其中![]()
设![]() ,即
,即![]() ,其中
,其中![]()
则![]() ,其中
,其中![]()
(1)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是增函数
是增函数
从而当![]() 时,
时, ![]() ,
,
所以![]() 是增函数,从而
是增函数,从而![]() .
.
故当![]() 时符合题意.
时符合题意.
(2)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上是减函数
上是减函数
从而当![]() 时,
时, ![]()
所以![]() 在
在![]() 上是减函数,从而
上是减函数,从而![]()
故当![]() 时不符合题意.
时不符合题意.
(3)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是减函数
是减函数
从而当![]() 时,
时, ![]()
所以![]() 是减函数,从而
是减函数,从而![]()
故当![]() 时不符合题意
时不符合题意
综上![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
22
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,长轴长为
,长轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 是以长轴为直径的圆
是以长轴为直径的圆![]() 上一点,圆
上一点,圆![]() 在点
在点![]() 处的切线交直线
处的切线交直线![]() 于点
于点![]() ,求证:过点
,求证:过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 过椭圆
过椭圆![]() 的右焦点.
的右焦点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,则下列判断正确的是( )
的部分图象如图所示,则下列判断正确的是( )
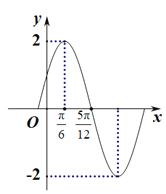
A. 函数的图象关于点![]() 对称
对称
B. 函数的图象关于直线![]() 对称
对称
C. 函数![]() 的最小正周期为
的最小正周期为![]()
D. 当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 围成的封闭图形面积为
围成的封闭图形面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 是
是![]() 所在平面内一点,下列说法正确的是( )
所在平面内一点,下列说法正确的是( )
A.若![]() ,则
,则![]() 的形状为等边三角形
的形状为等边三角形
B.若![]() ,则点
,则点![]() 是边
是边![]() 的中点
的中点
C.过![]() 任作一条直线,再分别过顶点
任作一条直线,再分别过顶点![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,若
,若![]() 恒成立,则点
恒成立,则点![]() 是
是![]() 的垂心
的垂心
D.若![]() 则点
则点![]() 在边
在边![]() 的延长线上
的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数函数g(x)=1ogax(a>0,a≠1)和指数函数f(x)=ax(a>0,a≠1)互为反函数.已知函数f(x)=3x,其反函数为y=g(x).
(Ⅰ)若函数g(kx2+2x+1)的定义域为R,求实数k的取值范围;
(Ⅱ)若0<x1<x2且|g(x1)|=|g(x2)|,求4x1+x2的最小值;
(Ⅲ)定义在I上的函数F(x),如果满足:对任意x∈I,总存在常数M>0,都有-M≤F(x)≤M成立,则称函数F(x)是I上的有界函数,其中M为函数F(x)的上界.若函数h(x)=![]() ,当m≠0时,探求函数h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范围,若不存在,请说明理由.
,当m≠0时,探求函数h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范围,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com