
【题目】已知点![]() 为平面内一定点,动点
为平面内一定点,动点![]() 为平面内曲线
为平面内曲线![]() 上的任意一点,且满足
上的任意一点,且满足![]() ,过原点的直线交曲线
,过原点的直线交曲线![]() 于
于![]() 两点.
两点.
(1)证明:直线![]() 与直线
与直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)设直线![]() ,
,![]() 交直线
交直线![]() 于
于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最小值.
长度的最小值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由题意可知点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,设
为焦点的椭圆,设![]() ,则
,则![]() ,可得
,可得![]() ,利用点在椭圆上可得定值;
,利用点在椭圆上可得定值;
(2)由(1)可设直线![]() :
:![]() ,则直线
,则直线![]() :
:![]() ,分别求出
,分别求出![]() 、
、![]() 的坐标,表示线段
的坐标,表示线段![]() 长度,利用均值不等式求最值即可.
长度,利用均值不等式求最值即可.
(1)设![]() ,
,![]() ,
,
由题意可知![]() ,且
,且![]() ,
,
所以,点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,且长轴长为4,焦距为
为焦点的椭圆,且长轴长为4,焦距为![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
所以,曲线![]() 的轨迹方程为
的轨迹方程为![]() .
.
由已知![]() 两点关于原点对称,不妨设
两点关于原点对称,不妨设![]() ,则
,则![]() ,
,
所以,![]() ,
,
又因为,点![]() 在曲线
在曲线![]() 上,所以,
上,所以,![]() ,解得,
,解得,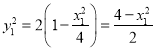 ,
,
所以,![]() ,
,
所以,直线![]() 与直线
与直线![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(2)由第(1)可得,![]() ,
,
所以,不妨设直线![]() :
:![]() ,则直线
,则直线![]() :
:![]() ,
,
将![]() 分别代入直线
分别代入直线![]() ,直线
,直线![]() 的方程得,
的方程得,![]() ,
,![]() ,
,
![]() ,
,
因为,![]() ,所以,
,所以,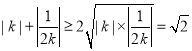 ,
,
当且仅当![]() ,即
,即![]() 时,取得最小值
时,取得最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛、马和羊,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,则让三位同学选取的礼物都满意的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 折起到
折起到![]() (
(![]() 平面
平面![]() )的位置,
)的位置,![]() 为线段
为线段![]() 的中点.
的中点.
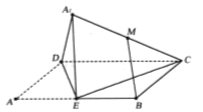
(1)求证:![]() 平面
平面![]() ;
;
(2)已知![]() ,当平面
,当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() 为正三角形, 侧面
为正三角形, 侧面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 的中点.
的中点.
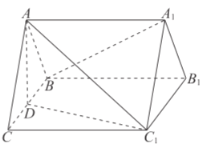
(1)求证![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高新企业自2012年成立以来,不断创新技术与产品,积极拓展市场,销售收入![]() (单位万元)与年份代号
(单位万元)与年份代号![]() 之间对应关系如下表,且满足回归函数
之间对应关系如下表,且满足回归函数![]() ,记
,记![]() 。
。
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 80 | 199 | 398 | 2512 | 6310 | 15848 | 79432 |
| 1.9 | 2.3 | 2.6 | 3.4 | 3.8 | 4.2 | 4.9 |
(1)任取2年对比销售收入的情况,求这2年中销售收入均超过400万元的概率;
(2)求回归函数![]() 中
中![]() 的值。
的值。
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
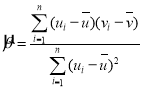 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com