
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() 为正三角形, 侧面
为正三角形, 侧面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 的中点.
的中点.
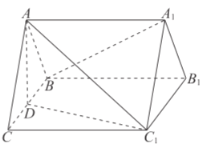
(1)求证![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
【答案】(1)证明见解析(2)![]() (3)直线
(3)直线![]() 与平面
与平面![]() 相交.证明见解析
相交.证明见解析
【解析】
(1)根据线面平行的判定定理,在面![]() 内找一条直线平行于
内找一条直线平行于![]() 即可.所以连接
即可.所以连接![]() 交
交![]() 与点
与点![]() ,再连接
,再连接![]() ,由中位线定理可得
,由中位线定理可得![]() ,即可得证;
,即可得证;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() .分别以
.分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,如图建立空间直角坐标系,再根据二面角的向量方法即可求出;
轴,如图建立空间直角坐标系,再根据二面角的向量方法即可求出;
(3)根据平面![]() 的法向量与直线
的法向量与直线![]() 的方向向量的关系,即可判断直线
的方向向量的关系,即可判断直线![]() 与平面
与平面![]() 的位置关系.
的位置关系.
(1)由题意,三棱柱![]() 为正三棱柱.
为正三棱柱.
连接![]() . 设
. 设![]() ,则
,则![]() 是
是![]() 的中点.连接
的中点.连接![]() , 由
, 由![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中点,得
的中点,得![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
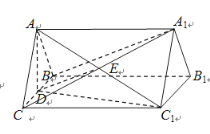
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]()
![]() 为正三角形,且
为正三角形,且![]() 为
为![]() 中点,所以
中点,所以![]() .
.
由![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中点,得
的中点,得![]() ,
,
又因为![]() 平面
平面![]() , 所以
, 所以![]() 平面
平面![]() ,即有
,即有![]() ,
,![]() .
.
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,如图建立空间直角坐标系,
轴,如图建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,得
,得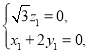
令![]() ,得
,得![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,得
,得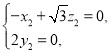
令![]() ,得
,得![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,则
,则 ![]() .
.
由图可得二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

(3)结论:直线![]() 与平面
与平面![]() 相交.
相交.
证明:因为![]() ,
,![]() ,且
,且![]() ,
,
所以![]() .
.
又因为平面![]() 的法向量
的法向量![]() ,且
,且![]() ,
,
所以![]() 与
与![]() 不垂直,
不垂直,
因为![]() 平面
平面![]() ,且
,且![]() 与平面
与平面![]() 不平行,
不平行,
故直线![]() 与平面
与平面![]() 相交.
相交.


科目:高中数学 来源: 题型:
【题目】某公司为了了解年研发资金投人量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.对公司近
(单位:亿元)的影响.对公司近![]() 年的年研发资金投入量
年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,进行了对比分析,建立了两个函数模型:①
的数据,进行了对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 均为常数,
均为常数,![]() 为自然对数的底数.并得到一些统计量的值.令
为自然对数的底数.并得到一些统计量的值.令![]() ,
,![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)若下一年销售额![]() 需达到
需达到![]() 亿元,预测下一年的研发资金投入量
亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数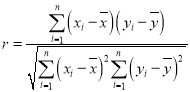 ,
,
回归直线![]() 中公式分别为:
中公式分别为: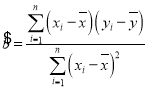 ,
,![]() ;
;
②参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)过点O作直线l的垂线,垂足为D.若![]() ,求动点D的轨迹方程.
,求动点D的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为平面内一定点,动点
为平面内一定点,动点![]() 为平面内曲线
为平面内曲线![]() 上的任意一点,且满足
上的任意一点,且满足![]() ,过原点的直线交曲线
,过原点的直线交曲线![]() 于
于![]() 两点.
两点.
(1)证明:直线![]() 与直线
与直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)设直线![]() ,
,![]() 交直线
交直线![]() 于
于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
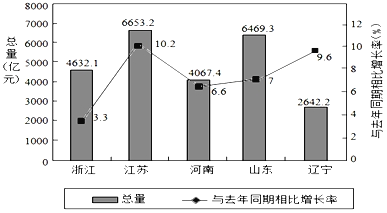
A.2017年第一季度GDP增速由高到低排位第5的是浙江省.
B.与去年同期相比,2017年第一季度的GDP总量实现了增长.
C.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D.去年同期河南省的GDP总量不超过4000亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,则数列
,则数列![]() 中第几项最小?请说明理由;
中第几项最小?请说明理由;
(3)若![]() (n=1,2,3,…),求证:“数列
(n=1,2,3,…),求证:“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() ,其中
,其中![]() ,同时满足:
,同时满足:
①![]() 在
在![]() 内是单调函数:②当定义域为
内是单调函数:②当定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,则称函数
,则称函数![]() 是区间
是区间![]() 上的“保值函数”,区间
上的“保值函数”,区间![]() 称为“保值函数”.
称为“保值函数”.
(1)求证:函数![]() 不是定义域
不是定义域![]() 上的“保值函数”;
上的“保值函数”;
(2)若函数![]() (
(![]() )是区间
)是区间![]() 上的“保值函数”,求
上的“保值函数”,求![]() 的取值范围;
的取值范围;
(3)对(2)中函数![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线
为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() .若直线
.若直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com