练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知y＝f(x)，x∈(－a，a)，F(x)＝f(x)＋f(－x)，则F(x)是（ ）
    A.奇函数
    B.偶函数
    C.既是奇函数又是偶函数
    D.非奇非偶函数

    【答案】B
    【解析】根据题意知F(－x)＝f(－x)＋f(x)＝F(x)，
    又x∈(－a，a)关于原点对称，∴F(x)是偶函数．
    所以答案是:B.
    【考点精析】认真审题，首先需要了解函数的奇偶性(偶函数的图象关于y轴对称；奇函数的图象关于原点对称)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)=(2a1)x ， 若x＞0时总有f(x)＞1，则实数a的取值范围是( )
    A.1＜a＜2
    B.a＜2
    C.a＞1
    D.0<a<1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）求经过直线l1：2x＋3y－5＝0与l2：7x＋15y＋1＝0的交点，且平行于直线x＋2y－3＝0的直线方程;

    （2）求与直线3x＋4y－7＝0垂直，且与原点的距离为6的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一次测验共有4个选择题和2个填空题，每答对一个选择题得20分，每答对一个填空题得10分，答错或不答得0分，若某同学答对每个选择题的概率均为，答对每个填空题的概率均为，且每个题答对与否互不影响.

    （1）求该同学得80分的概率；

    （2）若该同学已经答对了3个选择题和1个填空题，记他这次测验的得分为，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如（1）图所示，在直角梯形ABCD中，AD∥BC，，AB＝BC＝1，AD＝2，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到△A1BE的位置，如图（2）所示．

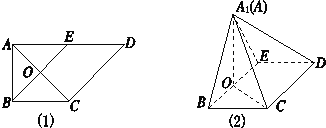
    （1）证明：CD⊥平面A1OC；

    （2）若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三棱锥P-A BC的四个顶点都在球D的表面上，PA⊥平面ABC，AB⊥BC，PA =3，AB=BC=2，则球O的表面积为（ ）

    A．13π B．17π C．52π D．68π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个直角三角形绕斜边所在直线旋转360°形成的空间几何体为（ ）
    A.一个圆锥
    B.一个圆锥和一个圆柱
    C.两个圆锥
    D.一个圆锥和一个圆台

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，为圆上的动点，定点，线段的垂直平分线交线段于点．

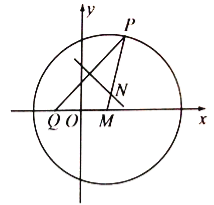
    （1）求动点的轨迹方程；

    （2）记动点的轨迹为曲线 ，设圆的切线交曲线于两点，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形的边长为2，分别为线段的中点，在五棱锥中，为棱的中点，平面与棱分别交于点．

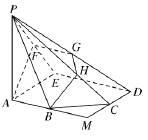
    （1）求证：；

    （2）若底面，且，求直线与平面所成角的大小．

    查看答案和解析>>

    同步练习册答案