解:(I)由f'(x)=ln(1+x)+

-a>0
得a<ln(1+x)+

,
令h(x)=ln(1+x)+

,则h'(x)=

+
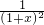
.
当x∈[1,+∞)时,h'(x)>0,h(x)在[1,+∞)上递增,
∴a<h(1)=

+ln2.
∴实数a的取值范围是(-∞,

+ln2).
(II)g(x)=ln(1+x)+

-a,x∈(-1,+∞)
则g'(x)=
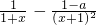
=

①当a>1时,x∈(-1,a-2),g'(x)<0,g(x)是减函数,
x∈(a-2,+∞)时,g'(x)>0,g(x)是增函数.
②当a≤1时,x∈(-1,+∞),g'(x)>0,g(x)是增函数.
所以:当a>1时,减区间为(-1,a-2),增区间为(a-2,+∞);
当a≤1时,增区间为(-1,+∞).
分析:(I)先把f'(x)=ln(1+x)+

-a>0转化为a<ln(1+x)+

,再利用导函数研究出不等式右边的单调性,进而求出其最值即可求出实数a的取值范围;
(II)先求出函数g(x)的导函数,分情况得到导函数值为正和为负对应的变量的取值范围,进而求出其单调区间.
点评:本题第二问主要研究利用导数研究函数的单调性.利用导数研究函数的单调性时,一般结论是:导数大于0对应区间为原函数的递增区间;导数小于0对应区间为原函数的递减区间.

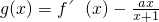 的单调区间.
的单调区间. -a>0
-a>0 ,
, ,则h'(x)=
,则h'(x)= +
+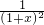 .
. +ln2.
+ln2. +ln2).
+ln2). -a,x∈(-1,+∞)
-a,x∈(-1,+∞)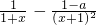 =
=
 -a>0转化为a<ln(1+x)+
-a>0转化为a<ln(1+x)+ ,再利用导函数研究出不等式右边的单调性,进而求出其最值即可求出实数a的取值范围;
,再利用导函数研究出不等式右边的单调性,进而求出其最值即可求出实数a的取值范围;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<