
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)证明:对于![]() ,
, ![]() 在区间
在区间![]() 上有极小值,且极小值大于0.
上有极小值,且极小值大于0.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析: (1)因为![]() ,
, ![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,代入化简即可; (2)因为
,代入化简即可; (2)因为![]() ,所以
,所以![]() 在区间
在区间![]() 上是单调递增函数.因为
上是单调递增函数.因为![]() ,
, ![]() , 所以
, 所以![]() ,使得
,使得![]() . 故
. 故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增, 所以
上单调递增, 所以![]() 有极小值
有极小值![]() .因为
.因为![]() ,所以
,所以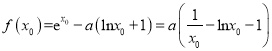 .构造函数求导判断单调性与最值即可得证.
.构造函数求导判断单调性与最值即可得证.
试题解析:(Ⅰ) ![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() ,
, ![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ) 因为![]() ,所以
,所以![]() 在区间
在区间![]() 上是单调递增函数.
上是单调递增函数.
因为![]() ,
, ![]() ,
,
所以![]() ,使得
,使得![]() .
.
所以![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 有极小值
有极小值![]() .
.
因为![]() ,
,
所以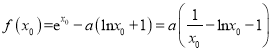 .
.
设![]() ,
, ![]() ,
,
则![]() ,
,
所以![]() ,
,
即![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
即![]() ,所以函数
,所以函数![]() 的极小值大于0.
的极小值大于0.
点睛:本题考查导数的几何意义以及函数的单调性与极值问题. 函数y=f(x)在x=x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,y0)处的切线的斜率![]() ,过点P的切线方程为:
,过点P的切线方程为: ![]() .求函数y=f(x)在点P(x0,y0)处的切线方程与求函数y=f(x)过点P(x0,y0)的切线方程意义不同,前者切线有且只有一条,且方程为y-y0=f′(x0)(x-x0),后者可能不只一条.
.求函数y=f(x)在点P(x0,y0)处的切线方程与求函数y=f(x)过点P(x0,y0)的切线方程意义不同,前者切线有且只有一条,且方程为y-y0=f′(x0)(x-x0),后者可能不只一条.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=bax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x)的表达式;
(2)设函数g(x)=f(x)﹣2×3x , 求g(x+1)>g(x)时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对![]() 名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在
名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在![]() 名男性驾驶员中,平均车速超过
名男性驾驶员中,平均车速超过![]()
![]() 的有
的有![]() 人,不超过
人,不超过![]()
![]() 的有
的有![]() 人;在
人;在![]() 名女性驾驶员中,平均车速超过
名女性驾驶员中,平均车速超过![]()
![]() 的有
的有![]() 人,不超过
人,不超过![]()
![]() 的有
的有![]() 人.
人.
(Ⅰ)完成下面的列联表,并判断是否有![]() 的把握认为平均车速超过100
的把握认为平均车速超过100![]() 与性别有关;
与性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶人数 | |||
女性驾驶人数 | |||
合计 |
(Ⅱ)在被调查的驾驶员中,按分层抽样的方法从平均车速不超过![]()
![]() 的人中抽取
的人中抽取![]() 人,再从这
人,再从这![]() 人中采用简单随机抽样的方法随机抽取
人中采用简单随机抽样的方法随机抽取![]() 人,求这
人,求这![]() 人恰好为
人恰好为![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
参考公式与数据:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log ![]() 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={y|y=( ![]() )x , x>0},Q={x|y=lg(2x﹣x2)},则(RP)∩Q为( )
)x , x>0},Q={x|y=lg(2x﹣x2)},则(RP)∩Q为( )
A.[1,2)
B.(1,+∞)
C.[2,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在![]() 轴正半轴上,准线
轴正半轴上,准线![]() 与圆
与圆![]() 相切.
相切.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和抛物线
和抛物线![]() 交于点
交于点![]() ,命题
,命题![]() :“若直线
:“若直线![]() 过定点(0,1),则
过定点(0,1),则 ![]() ”,
”,
请判断命题![]() 的真假,并证明.
的真假,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市卫生防疫部门为了控制某种病毒的传染,提供了批号分别为![]() 的五批疫苗,供全市所辖的
的五批疫苗,供全市所辖的![]() 三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
(1)求三个区注射的疫苗批号中恰好有两个区相同的概率;
(2)记![]() 三个区选择的疫苗批号的中位数为
三个区选择的疫苗批号的中位数为![]() ,求
,求 ![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com