
【题目】已知函数f(x)=bax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x)的表达式;
(2)设函数g(x)=f(x)﹣2×3x , 求g(x+1)>g(x)时x的取值范围.
【答案】
(1)解:把A(1,6),B(3,24)代入f(x)=bax,得
![]() ,结合a>0且a≠1,解得:
,结合a>0且a≠1,解得: ![]() ,
,
∴f(x)=32x
(2)解:由(1)得:g(x)=32x﹣2×3x,
g(x+1)=32x+1﹣2×3x+1,
由g(x+1)>g(x)得:
32x+1﹣23x+1﹣32x+23x>0,
∴32x﹣42x>0,
∴ ![]() >
> ![]() ,
,
解得:x< ![]()
【解析】(1)根据函数f(x)=bax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24),把A(1,6),B(3,24)代入f(x)=bax , 解此方程组即可求得a,b,的值,从而求得f(x);(2)求出g(x+1),g(x),问题转化为32x﹣42x>0,解出即可.


科目:高中数学 来源: 题型:
【题目】已知⊙![]() :
: ![]() 与⊙
与⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分别为左右焦点的椭圆
分别为左右焦点的椭圆![]() :
: ![]() 经过两圆的交点.
经过两圆的交点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,
的左右顶点, ![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上非顶点的三点,若
上非顶点的三点,若![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题
①奇函数的图象一定通过原点
②函数y= ![]() 是偶函数,但不是奇函数
是偶函数,但不是奇函数
③函数f(x)=ax﹣1+3的图象一定过定点P,则P点的坐标是(1,4)
④若f(x+1)为偶函数,则有f(x+1)=f(﹣x﹣1)
⑤若函数f(x)= 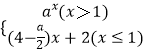 在R上的增函数,则实数a的取值范围为[4,8)
在R上的增函数,则实数a的取值范围为[4,8)
其中正确的命题序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水果树的产量![]() (单位:百千克)与肥料费用(单位:百元)满足如下关系:
(单位:百千克)与肥料费用(单位:百元)满足如下关系:  .此外,还需要投入其它成本(如施肥的人工费等)
.此外,还需要投入其它成本(如施肥的人工费等)![]() 百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为
百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求![]() 的函数关系式;
的函数关系式;
当投入的肥料费用为多少时,该水果树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,圆
,圆![]() :
: ![]() .直线
.直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() 两点,与圆
两点,与圆![]() 切于点
切于点![]() .
.
(1)当切点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 及圆
及圆![]() 的方程;
的方程;
(2)当![]() 时,证明:
时,证明: ![]() 是定值,并求出该定值.
是定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com