
【题目】已知⊙![]() :
: ![]() 与⊙
与⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分别为左右焦点的椭圆
分别为左右焦点的椭圆![]() :
: ![]() 经过两圆的交点.
经过两圆的交点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,
的左右顶点, ![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上非顶点的三点,若
上非顶点的三点,若![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() 的面积为定值3..
的面积为定值3..
【解析】试题分析:(Ⅰ)依题意有![]() ,由椭圆定义知
,由椭圆定义知![]() ,解得
,解得![]() 点值,得出椭圆的方程;
点值,得出椭圆的方程;
(Ⅱ)由题可知![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,把直线
,把直线![]() 的方程为
的方程为![]() 与椭圆方程联立,利用根与系数的关系和韦达定理,即可求
与椭圆方程联立,利用根与系数的关系和韦达定理,即可求![]() 面积的定值.
面积的定值.
试题解析:(Ⅰ)设两圆的交点为![]() ,依题意有
,依题意有![]() ,
,
由椭圆定义知![]() ,解得
,解得![]() ;
;
因为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左右焦点,所以
的左右焦点,所以![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)解法一 由题可知![]() ,
, ![]() ,设
,设![]() ,∵
,∵![]() 上的点,
上的点,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∵![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,∴
,∴![]() ,
,
∵![]() 、
、![]() 、
、![]() 是椭圆
是椭圆![]() 上非顶点的三点,∴直线
上非顶点的三点,∴直线![]() 的斜率存在且不为零,
的斜率存在且不为零,
设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
由 ,得
,得![]() ,
,
由![]() ,得
,得![]() (*)
(*)
且![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,整理得
,整理得![]() ,
,
代入(*)得![]() ,
,
∵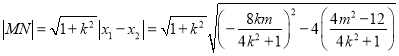
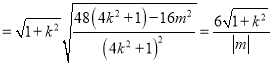 ,
,
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,∴
,∴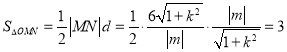 (定值).
(定值).
综上所述, ![]() 的面积为定值3.(Ⅱ)解法二 同解法一可知,直线
的面积为定值3.(Ⅱ)解法二 同解法一可知,直线![]() ,
, ![]() 的斜率存在且不为零,且
的斜率存在且不为零,且![]() ,……6分
,……6分
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
, ![]() ,
,
由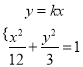 得
得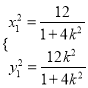 ,用
,用![]() 换
换![]() 可得
可得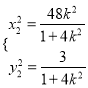 ,则
,则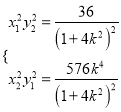 ,
,
因为![]() ,所以与
,所以与![]() 异号,
异号,
∴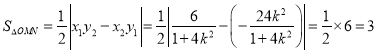 (定值).
(定值).
综上所述, ![]() 的面积为定值3.
的面积为定值3.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=2x2﹣4x.
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)用描点法画出它的图象;
(3)求出函数的最值,并分析函数的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 且
且![]() ,且,函数
,且,函数![]() 的图象与直线
的图象与直线![]() 相切.
相切.
(1)求![]() 的解析式;
的解析式;
(2)若当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在区间![]() ,使得
,使得![]() 在区间
在区间![]() 上的值域恰好为
上的值域恰好为![]() ?若存在,请求出区间
?若存在,请求出区间![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高考改革新方案,不分文理科,高考成绩实行“![]() ”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体
”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体![]() ,从学生群体
,从学生群体![]() 中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如下表:
中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如下表:

(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记![]() 表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量
表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)将频率视为概率,现从学生群体![]() 中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作
中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=2,直线CA与平面ABD所成角的正弦值为![]() ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,
, ![]() 于M、交EF于点N,
于M、交EF于点N, ![]() ,
, ![]() ,现将梯形ABCD沿EF折起,记折起后C、D为
,现将梯形ABCD沿EF折起,记折起后C、D为![]() 、
、![]() 且使
且使![]() ,如图示.
,如图示.
![]()
![]()

(Ⅰ)证明: ![]()
![]() 平面ABFE;,
平面ABFE;,
(Ⅱ)若图6中, ![]() ,求点M到平面
,求点M到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 共焦点
共焦点![]() ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于![]() ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足![]() .
.
(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点![]() 作抛物线的切线
作抛物线的切线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,设线段AB的中点为
两点,设线段AB的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=bax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x)的表达式;
(2)设函数g(x)=f(x)﹣2×3x , 求g(x+1)>g(x)时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com