
分析 (Ⅰ)利用辅助角公式化简,将已知函数解析式转化为正弦函数,根据正弦函数图象解答;
(Ⅱ)首项求得g(x)=2sin(2x+$\frac{π}{6}$),利用正弦函数图象解题.
解答 解:(Ⅰ)f(x)=sinx+$\sqrt{3}$cosx=2sin(x+$\frac{π}{3}$).
由2kπ-$\frac{π}{2}$≤x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$(k∈Z)
得:2kπ-$\frac{5π}{6}$≤x≤2kπ+$\frac{π}{6}$(k∈Z),故f(x)的单调递增区间是:[2kπ-$\frac{5π}{6}$,2kπ+$\frac{π}{6}$],k∈Z.
(Ⅱ)g(x)=[f(x)]2-2,
=4sin2(x+$\frac{π}{3}$)-2,
=4×$\frac{1}{2}$[1-cos(2x+$\frac{2π}{3}$)]-2,
=-2cos(2x+$\frac{2π}{3}$),
=2sin(2x+$\frac{π}{6}$).
∵x∈[0,$\frac{π}{4}$],
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],
∴g(x)=2sin(2x+$\frac{π}{6}$)的最大值是1,最小值是-2.
点评 本题考查三角函数中的恒等变换应用,正弦函数图象.利用三角函数公式将函数进行化简是解决本题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
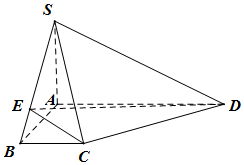 在如图所示的四棱锥S-ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E为线段BS上的一个动点.
在如图所示的四棱锥S-ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E为线段BS上的一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{24}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
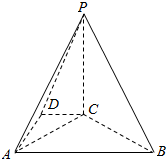 在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.
在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com