
���� �������֪�¶��弴��д���������������У�
�������2013�ס��ڴ����С��Ĺ���Ϊd��������ɵã�a1+a2+a3+��+a2013=0����ϵȲ����е����ʽ����a1+a2013=0���Ӷ������a1007=0�������ɵ�a1008=d����d��0��d��0�����������ͨ�ʽ��
����1���ж�k=nʱ��$|{S_k}|��\frac{1}{2}$��Ȼ��֤��k��nʱ��������������Լ�����ֵ���Dz���ʽ֤�����ɣ�
��2��ͨ��������ͣ��Լ�����ֵ���Dz���ʽ�ͷ����������������ͣ�����֤��$|{\sum_{i=1}^n{\frac{a_i}{i}}}|��\frac{1}{2}-\frac{1}{2n}$��
��� �⣺��������$-\frac{1}{2}��0��\frac{1}{2}$Ϊ����λ���С�1��
����$-\frac{3}{8}��-\frac{1}{8}��\frac{1}{8}��\frac{3}{8}$Ϊ�Ľ�λ���У���..��..3�֣�������������֣�
������Ȳ�����a1��a2��a3������a2k+1��k��1���Ĺ���Ϊd��
��a1+a2+a3+��+a2k+1=0��
��$��2k+1��{a_1}+\frac{2k��2k+1��d}{2}=0$��
��a1+kd=0��
��ak+1=0����ak+2=d����4��
��d=0ʱ���뵥λ���е������٢�ì�ܣ���5��
��d��0ʱ���ݵ�λ���е������٢ڵã�${a_{k+2}}+{a_{k+3}}+��+{a_{2k+1}}=\frac{1}{2}$��
��$kd+\frac{k��k-1��}{2}d=\frac{1}{2}����d=\frac{1}{k��k+1��}$
��ak+1=0��${a_1}+k•\frac{1}{k��k+1��}=0����{a_1}=-\frac{1}{k+1}$��
��${a_n}=-\frac{1}{k+1}+��n-1��\frac{1}{k��k+1��}=\frac{n}{k��k+1��}-\frac{1}{k}��n��{N^*}��n��2k+1��$����7��
��d��0ʱ��
ͬ���ɵ�$kd+\frac{k��k-1��}{2}d=-\frac{1}{2}����d=-\frac{1}{k��k+1��}$��
��ak+1=0����${a_1}-k•\frac{1}{k��k+1��}=0����{a_1}=\frac{1}{k+1}$��
��${a_n}=\frac{1}{k+1}-��n-1��\frac{1}{k��k+1��}=-\frac{n}{k��k+1��}+\frac{1}{k}��n��{N^*}��n��2n+1��$����8��
����֤������1����k=nʱ����Ȼ$|{S_n}|=0��\frac{1}{2}$��������9��
��k��nʱ���������ٵ�Sk=a1+a2+��+ak=-��ak+1+ak+2+��+an����
��|Sk|=|a1+a2+��+ak|=|ak+1+ak+2+��+an|��
��2|Sk|=|a1+a2+��+ak|+|ak+1+ak+2+��+an|��|a1|+|a2|+��+|ak|+|ak+1|+|ak+2|+��+|an|=1��
��$|{S_k}|��\frac{1}{2}��k=1��2��3������n��$����11��
$��2��|{\sum_{i=1}^n{\frac{a_i}{i}}}|=|{\frac{a_1}{1}+\frac{a_2}{2}+\frac{a_3}{3}+\frac{a_4}{4}+��+\frac{{{a_{n-1}}}}{n-1}+\frac{a_n}{n}}|$��
=$|{{S_1}+\frac{{{S_2}-{S_1}}}{2}+\frac{{{S_3}-{S_2}}}{3}+\frac{{{S_4}-{S_3}}}{4}+��+\frac{{{S_{n-1}}-{S_{n-2}}}}{n-1}+\frac{{{S_n}-{S_{n-1}}}}{n}}|$��
=$|{\frac{S_1}{2}+\frac{S_2}{2��3}+\frac{S_3}{3��4}+\frac{S_4}{4��5}+��+\frac{{{S_{n-1}}}}{��n-1��n}+\frac{S_n}{n}}|$��
$��|{\frac{S_1}{2}}|+|{\frac{S_2}{2��3}}|+|{\frac{S_3}{3��4}}|+|{\frac{S_4}{4��5}}|+��+|{\frac{{{S_{n-1}}}}{��n-1��n}}|$��
$��\frac{1}{2}��{\frac{1}{2}+\frac{1}{2��3}+\frac{1}{3��4}+\frac{1}{4��5}+��+\frac{1}{��n-1��n}}��$��
=$\frac{1}{2}��{\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+��+\frac{1}{n-1}-\frac{1}{n}}��$��
=$\frac{1}{2}-\frac{1}{2n}$����13�֣�
���� ���⿼���������¶����Ӧ�ã�������͵ķ������������Լ�����ֵ���Dz���ʽ��Ӧ�ã��������������������������ѶȽϴ�������������������⣮


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | -$\sqrt{3}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | -$\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | -$\frac{1}{5}$ | C�� | -$\frac{5}{13}$ | D�� | $\frac{5}{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
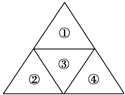 ��ͼ��Ҫ���٣��ڣ��ۣ����Ŀ�����ֱ�Ϳ�����ֲ�ͬ��ɫ�е�ijһ�֣�����ͬһ����ɫʹ�ö�Σ��������������Ϳ��ͬ��ɫ����ͬ��Ϳɫ��������Ϊ��������
��ͼ��Ҫ���٣��ڣ��ۣ����Ŀ�����ֱ�Ϳ�����ֲ�ͬ��ɫ�е�ijһ�֣�����ͬһ����ɫʹ�ö�Σ��������������Ϳ��ͬ��ɫ����ͬ��Ϳɫ��������Ϊ��������| A�� | 320 | B�� | 160 | C�� | 96 | D�� | 60 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com