
分析 (1)利用双曲线的渐近线与直线平行求出b,然后求出a,c即可求解双曲线的离心率.
(2)设出直线方程,联立直线与双曲线方程,通过向量相等,然后求解b,即可求解双曲线的方程.
解答 解:(1)因为双曲线的渐近线$y=±\frac{b}{a}x$$⇒\frac{b}{a}=1$,又因为$a=\sqrt{2}$,所以$b=\sqrt{2}$,
∴$e=\frac{c}{a}=\frac{{\sqrt{{a^2}+{b^2}}}}{a}=\frac{{\sqrt{2+2}}}{2}=\sqrt{2}$.
(2)F2(c,0),直线l:y=x-c,$\left\{{\begin{array}{l}{y=x-c}\\{\frac{x^2}{2}-\frac{y^2}{b^2}=1}\end{array}}\right.$,
(b2-2)y2+2cb2y+b2c2-2b2=0,所以$\left\{{\begin{array}{l}{{y_1}+{y_2}=\frac{{-2c{b^2}}}{{{b^2}-2}}}\\{{y_1}{y_2}=\frac{{{b^2}{c^2}-2{b^2}}}{{{b^2}-2}}}\end{array}}\right.$,
因为$\overrightarrow{FP}=\frac{1}{5}\overrightarrow{FQ}$,所以${y_1}=\frac{1}{5}{y_2}$,整理得:$\frac{{{c^2}{b^4}}}{{9({b^2}-2)}}=\frac{{{b^2}{c^2}-2{b^2}}}{5}$,
因为b2>0,所以c2-2=b2,$\frac{{{b^2}+2}}{{9({b^2}-2)}}=\frac{1}{5}$,所以b2=7,
所以双曲线C:$\frac{x^2}{2}-\frac{y^2}{7}=1$.
点评 本题考查双曲线的简单性质的应用,双曲线方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
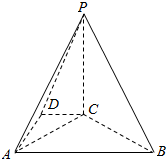 在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.
在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
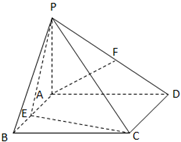 四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形.E、F分别是AB、PD的中点.若PA=AD=3,CD=$\sqrt{6}$,
四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形.E、F分别是AB、PD的中点.若PA=AD=3,CD=$\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{3}$和$\frac{22π}{3}$ | B. | $-\frac{7π}{9}$和$\frac{11π}{9}$ | C. | $\frac{20π}{3}$和$\frac{22π}{9}$ | D. | $\frac{π}{2}$和$-\frac{π}{2}+2kπ,k∈Z$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com