
【题目】设直线 ![]() 的方程为
的方程为 ![]() ,
, ![]() .
.
(1)若 ![]() 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求 ![]() 的方程;
的方程;
(2)若 ![]() 与两坐标轴围成的三角形的面积为6,求
与两坐标轴围成的三角形的面积为6,求 ![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(Ⅰ)求证:数列{ ![]() }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(Ⅱ)设bn+an=l(n∈N*),Sn=b1b2+b2b3+…+bnbn+1 , 试比较an与8Sn的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为1的正方形 ![]() 与
与 ![]() 所在的平面互相垂直,点
所在的平面互相垂直,点 ![]() 分别是线段
分别是线段 ![]() 上的动点(包括端点),
上的动点(包括端点), ![]() ,设线段
,设线段 ![]() 的中点的轨迹为
的中点的轨迹为 ![]() ,则
,则 ![]() 的长度为( )
的长度为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
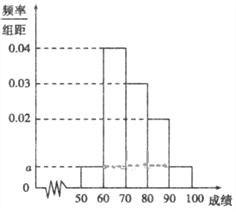
【题目】某校![]() 名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:
名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1).求图中![]() 的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
(2).若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如上右表所示,求数学成绩在
)之比如上右表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某市2017年2月28天的日空气质量指数折线图.
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅰ)请根据所给的折线图补全如图2所示的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com