
【题目】已知数列{an}中,a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(Ⅰ)求证:数列{ ![]() }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(Ⅱ)设bn+an=l(n∈N*),Sn=b1b2+b2b3+…+bnbn+1 , 试比较an与8Sn的大小.
【答案】解:(Ⅰ)∵an+1= ![]() (n∈N*),
(n∈N*),
∴ ![]() =
= ![]() =
= ![]() =﹣1,
=﹣1,
又 ![]() =
= ![]() ,
,
∴数列{ ![]() }是首项为﹣4,公差为﹣1的等差数列.
}是首项为﹣4,公差为﹣1的等差数列.
∴ ![]() ,化为
,化为 ![]() (n∈N*).
(n∈N*).
(Ⅱ)∵bn+an=l(n∈N*),
∴bn=1﹣an= ![]() ,
,
∴ ![]() ,
,
∴S=b1b2+b2b3+…+bnbn+1= ![]() +…+
+…+ ![]() =
= ![]() =
= ![]() ,
,
从而an﹣8Sn= ![]() =
= ![]() ,
,
∴当n≤2时,an>8Sn;
当n≥3时,an<8Sn.
【解析】(1)表示出![]() 和
和![]() ,进行作差得出其为定值-4,再由等差数列的通项公式可得到
,进行作差得出其为定值-4,再由等差数列的通项公式可得到![]() 的通项公式,(2)表示出
的通项公式,(2)表示出![]() ,由裂项求和得到S,进行作差可得到当n≤2时,an>8Sn;当n≥3时,an<8Sn.
,由裂项求和得到S,进行作差可得到当n≤2时,an>8Sn;当n≥3时,an<8Sn.
【考点精析】解答此题的关键在于理解等差关系的确定的相关知识,掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系 .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ,且
,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)将函数 ![]() 的图像向右平移
的图像向右平移 ![]() 个单位长度得到函数
个单位长度得到函数 ![]() 的图像,若函数
的图像,若函数 ![]() 在
在 ![]() 上有零点,求
上有零点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xoy中,直线l的参数方程是 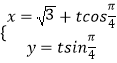 (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中 ![]() 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有 ![]() 是“年轻人”.
是“年轻人”.
(1)请你根据已知的数据,填写下列 ![]() 列联表:
列联表:
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | |||
不常使用单车用户 | |||
合计 |
(2)请根据(1)中的列联表,计算 ![]() 值并判断能否有
值并判断能否有 ![]() 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?
(附: ![]()
当 ![]() 时,有
时,有 ![]() 的把握说事件
的把握说事件 ![]() 与
与 ![]() 有关;当
有关;当 ![]() 时,有
时,有 ![]() 的把握说事件
的把握说事件 ![]() 与
与 ![]() 有关;当
有关;当 ![]() 时,认为事件
时,认为事件 ![]() 与
与 ![]() 是无关的)
是无关的)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com