
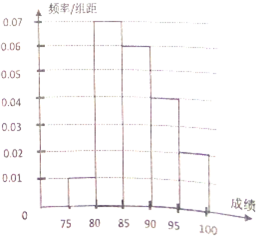
 2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.
2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.分析 (Ⅰ)先判断中位数落在第3组,设中位数距离85为x,则$\frac{0.1}{0.3}$=$\frac{x}{5}$,即可求出中位数,
(Ⅱ)根据分层抽样的定义即可求出答案.
(Ⅲ)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
解答 解:(Ⅰ)第1组的频率为0.01×5=0.05,第2组的频率为0.07×5=0.35,第3组的频率为0.06×5=0.30,
所以中位数落在第3组.
设中位数距离85为x,则$\frac{0.1}{0.3}$=$\frac{x}{5}$,解得x=$\frac{5}{3}$
故估计参加“华约”联盟笔试成绩的中位数87,
(Ⅱ)第4组的频率为0.04×5=0.2,第五组的频率为0.02×5=0.1,
则第4组与第五组的比为2:1,
故第4组抽取的人数为6×$\frac{2}{3}$=4人,第5组抽取的人数为6×$\frac{1}{3}$=2,
(Ⅲ)设第4组所抽取的4人分别为a,b,c,d,第5组的人数为A,B,从这6名学生中任取2人参加答辩环节,
共有ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB共15种情况,
这两人来自同一组的基本事件为ab,ac,ad,bc,bd,cd,AB共7种情况,
故这两人来自同一组的概率为$\frac{7}{15}$
点评 本题考查中位数的求法,考查概率的计算,解题时要认真审题,注意频率分布直方图的合理运用.是中档题


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d>p | B. | d<p | C. | d=p | D. | 无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
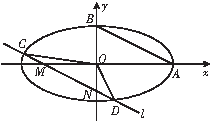 如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.
如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com