
分析 由题意画出图形,数形结合可知,当过椭圆中心O的直线为y轴上时,△F1AB面积的最大,由此求得△F1AB面积的最大值.
解答 解:如图,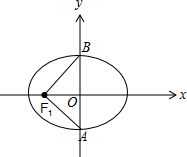
由图可知,当过椭圆中心O的直线为y轴上时,△F1AB面积的最大,
由$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,得a=5,b=4,则c=3.
∴${S}_{△A{F}_{1}B}={S}_{△O{F}_{1}B}+{S}_{△O{F}_{1}A}$=$\frac{1}{2}|O{F}_{1}|(|OA|+|OB|)=\frac{1}{2}×3×8=12$.
故答案为:12.
点评 本题考查椭圆的简单性质,考查了数形结合的解题思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
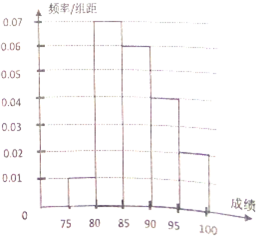 2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.
2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},1)$ | B. | $(-\frac{1}{2},1)$ | C. | $(\frac{1}{2},-1)$ | D. | $(-\frac{1}{2},-1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow a$•$\overrightarrow b$是一个向量 | C. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | D. | 0•$\overrightarrow{AB}$=$\overrightarrow 0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com