
分析 (1)把原不等式化为$\frac{1}{2}+a•{2}^{x-1}>x•{2}^{x-1}$>0,进一步转化为$a>x-\frac{1}{{2}^{x}}$(x>0)有解,利用函数单调性求出$x-\frac{1}{{2}^{x}}$在(0,+∞)上的范围得答案;
(2)f(x)当x∈(-∞,1]时有意义的条件是1+2x+…+nxa>0,x∈(-∞,1],n≥2恒成立.分离参数a,可得a>-[$(\frac{1}{n})^{x}+(\frac{2}{n})^{x}+…+(\frac{n-1}{n})^{x}$]恒成立,
利用函数单调性求得y=-[$(\frac{1}{n})^{x}+(\frac{2}{n})^{x}+…+(\frac{n-1}{n})^{x}$]在(-∞,1]上的最大值得答案.
解答 解:(1)当n=2时,不等式f(x)>lg(x2x-1)化为$lg\frac{1+a•{2}^{x}}{2}>lg(x{2}^{x-1})$,
即$\frac{1}{2}+a•{2}^{x-1}>x•{2}^{x-1}$>0,
∵2x-1>0,∴等价于$a>x-\frac{1}{{2}^{x}}$(x>0)有解,
∵y=x与y=$-\frac{1}{{2}^{x}}$在(0,+∞)上都是增函数,则y=x-$\frac{1}{{2}^{x}}$在(0,+∞)上是增函数,
而$x-\frac{1}{{2}^{x}}>0-\frac{1}{{2}^{0}}=-1$,
∴要使n=2时不等式f(x)>lg(x2x-1)有解,则实数a的取值范围为(-1,+∞);
(2)f(x)当x∈(-∞,1]时有意义的条件是1+2x+…+nxa>0,x∈(-∞,1],n≥2恒成立.
即a>-[$(\frac{1}{n})^{x}+(\frac{2}{n})^{x}+…+(\frac{n-1}{n})^{x}$]恒成立,
∵y=-$(\frac{k}{n})^{x}$,k=1,2,3,…,n-1在(-∞,1]上都是增函数,
∴y=-[$(\frac{1}{n})^{x}+(\frac{2}{n})^{x}+…+(\frac{n-1}{n})^{x}$]在(-∞,1]上都是增函数,
从而当x=1时,${y}_{max}=-(\frac{1}{n}+\frac{2}{n}+…+\frac{n-1}{n})=-\frac{1}{2}(n-1)$.
∴a>-[$(\frac{1}{n})^{x}+(\frac{2}{n})^{x}+…+(\frac{n-1}{n})^{x}$](n≥2)恒成立,只需a$>-\frac{1}{2}$.
故实数a的取值范围是(-$\frac{1}{2}$,+∞).
点评 本题考查函数的性质的应用,考查了不等式恒成立问题,关键是注意利用单调性求解最值问题,是中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
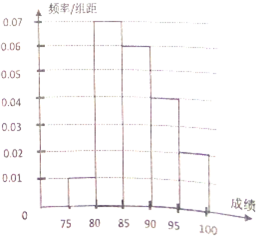 2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.
2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}-4}{10}$ | B. | $\frac{3\sqrt{3}+4}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},1)$ | B. | $(-\frac{1}{2},1)$ | C. | $(\frac{1}{2},-1)$ | D. | $(-\frac{1}{2},-1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow a$•$\overrightarrow b$是一个向量 | C. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | D. | 0•$\overrightarrow{AB}$=$\overrightarrow 0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com