
分析 (1)求出第一次抽到次品的事件数,求出总数,即可求解概率.
(2)求出第一次和第二次抽到次品的事件数,求出总数,即可求解概率.
解答 解、设第一次抽到次品为事件A,第二次抽到次品为事件B (2分)
(1)第一次抽到次品的概率$P(A)=\frac{{A_5^1A_{19}^1}}{{A_{20}^2}}=\frac{1}{4}$,
故第一次抽到次品的概率是$\frac{1}{4}$ (6分)
(2)第一次和第二次都抽到次品的概率$P(AB)=\frac{A_5^2}{{A_{20}^2}}=\frac{1}{19}$,
故第一次和第二次都抽到次品的概率是$\frac{1}{19}$.(12分)
点评 本题考查古典概型的概率的求法,考查计算能力.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
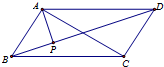 如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com