
分析 (1)利用椭圆结果的点以及离心率列出方程组,求解a,b即可得到椭圆方程.
(2)设直线l的方程为:$y=kx+\sqrt{2}$,通过$\left\{{\begin{array}{l}{y=kx+\sqrt{2}}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.⇒$$(\frac{1}{2}+{k^2}){x^2}+2\sqrt{2}kx+1=0$.令P(x1,y1),Q(x2,y2),利用判别式以及韦达定理,通过向量关系求解直线的斜率即可.
解答 解:(1)设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
依题意得$\left\{{\begin{array}{l}{{a^2}={b^2}+{c^2}}\\{\frac{c}{a}=\frac{{\sqrt{2}}}{2}}\\{\frac{1}{a^2}+\frac{1}{{2{b^2}}}=1}\end{array}}\right.$解得a2=2,b2=1.
所以椭圆C的方程为$\frac{x^2}{2}+{y^2}=1$.
(2)假设存在过点$(0,\sqrt{2})$且斜率为k的直线l适合题意,
则因为直线l的方程为:$y=kx+\sqrt{2}$,于是联立方程,
$\left\{{\begin{array}{l}{y=kx+\sqrt{2}}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.⇒$$(\frac{1}{2}+{k^2}){x^2}+2\sqrt{2}kx+1=0$.
由直线l与椭圆C交于不同两点P和Q知,$△=8{k^2}-4(\frac{1}{2}+{k^2})$=4k2-2>0,
∴${k^2}>\frac{1}{2}$.
令P(x1,y1),Q(x2,y2),∴$\overrightarrow{OP}+\overrightarrow{OQ}=({x_1}+{x_2},{y_1}+{y_2})$,
∵${x_1}+{x_2}=-\frac{{4\sqrt{2}k}}{{1+2{k^2}}}$,${y_1}+{y_2}=k({x_1}+{x_2})+2\sqrt{2}$=$\frac{{2\sqrt{2}}}{{1+2{k^2}}}$,
∴$\overrightarrow{OP}+\overrightarrow{OQ}=(-\frac{{4\sqrt{2}k}}{{1+2{k^2}}},\frac{{2\sqrt{2}}}{{1+2{k^2}}})$=$\frac{{2\sqrt{2}}}{{1+2{k^2}}}(-2k,1)$,
由题知${A_2}(\sqrt{2},0)$,B(0,1),$\overrightarrow{{A_2}B}(-\sqrt{2},1)$.
从而,根据向量$\overrightarrow{OP}+\overrightarrow{OQ}$与A2B共线,可得$2k=\sqrt{2}$,$k=\frac{{\sqrt{2}}}{2}$,这与${k^2}>\frac{1}{2}$矛盾.
故不存在符合题意的直线l.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,解析几何与向量的应用,设而不求方法的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{15}$ | B. | -$\frac{8}{15}$ | C. | $\frac{15}{17}$ | D. | -$\frac{15}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )| A. |  | B. | 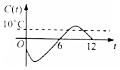 | C. | 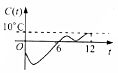 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| lnx | 0 | 0.69 | 1.10 | 1.39 | 1.61 |
| x-2 | -1 | 0 | 1 | 2 | 3 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 26 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com