
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=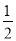 PD.
PD.
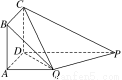
(1)证明:PQ⊥平面DCQ;
(2)求棱锥Q?ABCD的体积与棱锥P?DCQ的体积的比值.[来
(1)祥见解析; (2)1.
【解析】
试题分析:(1)要证直线与平面垂直,只须证明直线与平面内的两条相交直线垂直即可,注意到QA⊥平面ABCD,所以有平面PDAQ⊥平面ABCD,且交线为AD,又因为四边形ABCD为正方形,由面面垂直的性质可得DC⊥平面PDAQ,从而有PQ⊥DC,又因为PD∥QA,且QA=AB=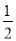 PD ,所以四边形PDAQ为直角梯形,利用勾股定理的逆定理可证PQ⊥QD;从而可证 PQ⊥平面DCQ;(2)设AB=a,则由(1)及已知条件可用含a的式子表示出棱锥Q-ABCD的体积和棱锥P-DCQ的体积从而就可求出其比值.
PD ,所以四边形PDAQ为直角梯形,利用勾股定理的逆定理可证PQ⊥QD;从而可证 PQ⊥平面DCQ;(2)设AB=a,则由(1)及已知条件可用含a的式子表示出棱锥Q-ABCD的体积和棱锥P-DCQ的体积从而就可求出其比值.
试题解析:(1)证明:由条件知PDAQ为直角梯形.
因为QA⊥平面ABCD,所以平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,
所以DC⊥平面PDAQ.可得PQ⊥DC.
在直角梯形PDAQ中可得DQ=PQ=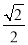 PD,
PD,
则PQ⊥QD.所以PQ⊥平面DCQ.
(2)设AB=a.由题设知AQ为棱锥Q?ABCD的高,所以棱锥Q-ABCD的体积V1=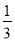 a3.
a3.
由(1)知PQ为棱锥P-DCQ的高,而PQ=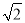 a,△DCQ的面积为
a,△DCQ的面积为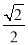 a2,
a2,
所以棱锥P-DCQ的体积V2=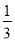 a3.
a3.
故棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值为1.
考点:1.线面垂直;2.几何体的体积.


科目:高中数学 来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
如图在△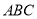 中,
中, ∥
∥ ,
, ,
, 交于点
交于点 ,则图中相似三角形的对数为( ).
,则图中相似三角形的对数为( ).

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
工人工资(元)依劳动生产率(千元)变化的回归方程为y=50+80x,下列判断中正确的是( )
A.劳动生产率为1000元时,工资为130元
B.劳动生产率平均提高1000元时,工资平均提高80元
C.劳动生产率平均提高1000元时,工资平均提高130元
D.当工资为250元时,劳动生产率为2000元
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知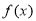 是定义在
是定义在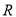 上的偶函数,且
上的偶函数,且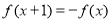 ,若
,若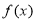 在
在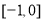 上单调递减,则
上单调递减,则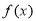 在
在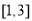 上是( )
上是( )
A.增函数 B.减函数
C.先增后减的函数 D.先减后增的函数
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
已知正三角形内切圆的半径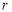 与它的高
与它的高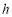 的关系是:
的关系是: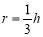 ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径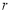 与正四面体高
与正四面体高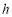 的关系是 .
的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com