
在四棱锥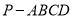 中,
中,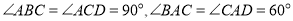 ,
, 平面
平面 ,
, 为
为 的中点,
的中点,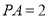 ,
,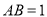 .
.
(Ⅰ)求四棱锥 的体积
的体积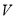 ;
;
(Ⅱ)若 为
为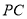 的中点,求证:平面
的中点,求证:平面 平面
平面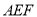 .
.
(Ⅰ)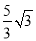 (Ⅱ)见解析
(Ⅱ)见解析
【解析】
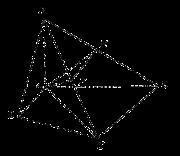
试题分析:(Ⅰ)由 平面
平面 知PA是棱锥P—ABCD的高,在Rt△ABC中,由AB=1,∠BAC=60o求出BC、BC,从而求出△ABC的面积,同理求出△ACD的面积,即可计算出四边形ABCD的面积,代入棱锥体积公式求出棱锥P—ABCD的体积;(Ⅱ)由由
知PA是棱锥P—ABCD的高,在Rt△ABC中,由AB=1,∠BAC=60o求出BC、BC,从而求出△ABC的面积,同理求出△ACD的面积,即可计算出四边形ABCD的面积,代入棱锥体积公式求出棱锥P—ABCD的体积;(Ⅱ)由由 平面
平面 知,PA⊥CD,由CD⊥AC,知CD⊥面PAC,因为E、F分别为PD、PC的中点,所以EF∥CD,由线面垂直性质得EF⊥面PAC,因为EF在面PAC内,根据面面垂直判定定理得面PAC⊥面AEF.
知,PA⊥CD,由CD⊥AC,知CD⊥面PAC,因为E、F分别为PD、PC的中点,所以EF∥CD,由线面垂直性质得EF⊥面PAC,因为EF在面PAC内,根据面面垂直判定定理得面PAC⊥面AEF.
试题解析:(Ⅰ)在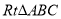 中,
中,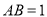 ,
, ,
,
∴  2分
2分
在 中,
中,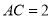 ,
,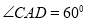 ,
,
 4分
4分
∵  ,
,
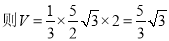 6分
6分
(Ⅱ)∵  , ∴
, ∴ 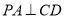 7分
7分
又 ,
,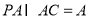
∴ 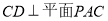 , 8分
, 8分
∵  ,∴
,∴ 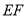 //
//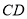
∴ 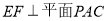 10分
10分
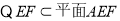 ,∴
,∴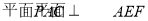 12分
12分
考点:棱锥的体积公式,线面垂直的判定与性质,面面垂直的判定,推理论证能力,运算求解能力


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源:2015届河北省保定市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格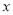 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式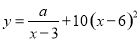 ,其中
,其中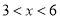 ,
,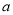 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求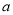 的值;
的值;
(2)若该商品的成品为3元/千克, 试确定销售价格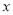 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一理科数学试卷(解析版) 题型:选择题
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有 ( )
A.36种 B.30种 C.24种 D.6种
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一文科数学试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)求 的解集;
的解集;
(Ⅱ)设函数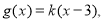
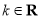 ,若
,若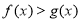 对任意的
对任意的 都成立,求
都成立,求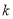 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一文科数学试卷(解析版) 题型:填空题
已知函数 的图像为曲线C,若曲线C存在与直线
的图像为曲线C,若曲线C存在与直线 垂直的切线,则实数
垂直的切线,则实数 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一文科数学试卷(解析版) 题型:选择题
过抛物线 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点,点
两点,点 是原点,若
是原点,若 ,则
,则 的面积为( )
的面积为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届河北唐山一中高二下学期期末考试理科数学试卷(解析版) 题型:选择题
定义域为R的函数 满足
满足 ,当
,当 [0,2)时,
[0,2)时, 若
若 时,
时, 有解,则实数t的取值范围是
有解,则实数t的取值范围是
A.[-2,0) (0,l) B.[-2,0)
(0,l) B.[-2,0)  [l,+∞) C.[-2,l] D.(
[l,+∞) C.[-2,l] D.( ,-2]
,-2] (0,l]
(0,l]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com