
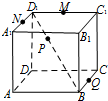
 ������ABCD-A1B1C1D1�У�M��N��Q�ֱ�����D1C1��A1D1��BC���е㣬��P�ڶԽ���BD1�ϣ������������⣺
������ABCD-A1B1C1D1�У�M��N��Q�ֱ�����D1C1��A1D1��BC���е㣬��P�ڶԽ���BD1�ϣ������������⣺| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� ��MN�е�R��AC���е�S����BD1��RS�Ľ�����Q����P��Q�غ�ʱ����ʱMN��ƽ��PAC�ڣ������жϳ�����
����A��P��M���㹲�ߣ���D1M��AB����ƽ���ߵ����ʿɵã�$\frac{{D}_{1}P}{BP}$=$\frac{{D}_{1}M}{AB}$=$\frac{1}{2}$�������жϳ�����
����$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$���ɢڿɵã�A��P��M���㹲�ߣ���Խ���BD��AC=O���ɵ��ı���OQC1M��ƽ���ı��Σ�����C1Q��OM�������жϳ�����
��������P�����������ʮ���������ɵĽǶ���ȵ�ֱ����A1C��D1B��AC1��DB1��4��������P����ֱ��AB1��A1C1���ɵĽǶ�Ϊ60���ֱ������ֻ��3���������жϳ�����
��� �⣺��MN�е�R��AC���е�S����BD1��RS�Ľ�����Q����P��Q�غ�ʱ����ʱMN��ƽ��PAC�ڣ���1����
����A��P��M���㹲�ߣ�����A��P��M���㹲�ߣ���D1M��AB��
��$\frac{{D}_{1}P}{BP}$=$\frac{{D}_{1}M}{AB}$=$\frac{1}{2}$����$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$����ȷ��
����$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$���ɢڿɵã�A��P��M���㹲�ߣ���Խ���BD��AC=O������OM��OQ�����ı���OQC1M��ƽ���ı��Σ�
��C1Q��OM��
��M����ƽ��APC�ڣ�
��C1Q��ƽ��APC�������ȷ��
��������P�����������ʮ���������ɵĽǶ���ȵ�ֱ����A1C��D1B��AC1��DB1��4����
����B1C��A1C1��AC��������������ʿɵá�AB1C�ǵȱ������Σ����Pȡ��D1����ֱ��AD1��CD1��D1B1���������������P����ֱ��AB1��A1C1���ɵĽǶ�Ϊ60���ֱ������ֻ��3������m+n=7���������ȷ��
������ȷ����Ϊ�ڢۢܣ������Ϊ3��
��ѡ��C��
���� ���⿼��������������ʡ�ƽ���߷��߶γɱ�������������ƽ�е��ж������ʶ������ռ�ǣ������˿ռ�������������������������������������⣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{0��\frac{1}{e}}]$ | B�� | $��{0��\frac{3}{4}}]$ | C�� | $[{\frac{1}{e}��1}��$ | D�� | $[{\frac{1}{e}��\frac{3}{4}}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com