
| A. | $({0,\frac{1}{e}}]$ | B. | $({0,\frac{3}{4}}]$ | C. | $[{\frac{1}{e},1})$ | D. | $[{\frac{1}{e},\frac{3}{4}}]$ |
分析 若a<$\frac{1}{e}$,则当x=a时,函数取极大值f(a)=-alna<$\frac{1}{e}}$,不满足条件,结合函数的零点$\frac{3}{4}$∈(a,1],可得答案.
解答 解:∵f(x)=$\left\{\begin{array}{l}-xlnx,0<x≤a\\ \frac{1}{e}cos2πx,a<x≤1\end{array}$,
∴f′(x)=$\left\{\begin{array}{l}{-lnx-1,0<x≤a}\\{-\frac{2π}{e}sin2πx,a<x≤1}\end{array}\right.$,
若a<$\frac{1}{e}$,则当x=a时,函数取极大值f(a)=-alna<$\frac{1}{e}}$,
当b∈(-alna,$\frac{1}{e}}$)时,函数g(x)=f(x)-b有且只有一个零点,
故a≥$\frac{1}{e}}$,
令f(x)=0,x∈(0,1],则x=$\frac{3}{4}$,
故$\frac{3}{4}$∈(a,1],即a≤$\frac{3}{4}$,
综上可得:a∈$[{\frac{1}{e},\frac{3}{4}}]$,
故选:D
点评 本题考查的知识点是函数零点,分段函数的应用,利用导数研究函数的极值,难度中档.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
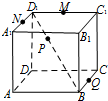 正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在对角线BD1上,给出以下命题:
正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在对角线BD1上,给出以下命题:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com