
分析 由2222=317×7+3,5555=793×7+4可得2222≡3 (mod 7),5555≡4 (mod 7),进而可得22225≡-55552(mod 7),进而可得(22225)1111+(55552)1111≡0(mod 7),证得结论.
解答 证明:∵22225555+55552222=(22225)1111+(55552)1111,
∵2222=317×7+3,5555=793×7+4;
∴2222≡3 (mod 7),5555≡4 (mod 7),
∴22225≡35≡5(mod 7),55552≡42≡2(mod 7),
∴22225+55552≡5+2≡0(mod 7),
∴22225≡-55552(mod 7),
∴(22225)1111≡(-55552)1111≡-(55552)1111(mod 7),
∴(22225)1111+(55552)1111≡0(mod 7),
即7|(22225555+55552222)
点评 本题考查的知识点是整除的基本性质,难度中档.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
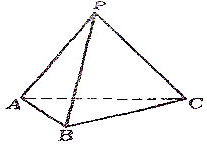 如图,点P是△ABC在平面外的一点,PA=PB=PC=2,AB=BC=AC=1,
如图,点P是△ABC在平面外的一点,PA=PB=PC=2,AB=BC=AC=1,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | ($\frac{1}{2}$,+∞) | D. | [$\frac{3}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{e}}]$ | B. | $({0,\frac{3}{4}}]$ | C. | $[{\frac{1}{e},1})$ | D. | $[{\frac{1}{e},\frac{3}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com