
分析 求出命题p、q为真命题时,实数m满足的条件,由p∨q为真命题且p∧q为假命题时,p,q一真一假;从而求出m的取值范围.
解答 解:命题p为真时,实数m满足$\left\{\begin{array}{l}{△>0}\\{-m<0}\end{array}\right.$,即$\left\{\begin{array}{l}{{m}^{2}-4>0}\\{m>0}\end{array}\right.$,解得m>2;
命题q为真时,实数m满足m∈(1,3),即1<m<3;
p∨q为真命题且p∧q为假命题时,p,q一真一假;
①若p真且q假,则实数m满足$\left\{\begin{array}{l}{m>2}\\{m≤1或m≥3}\end{array}\right.$,解得m≥3;
②若p假且q真,则实数m满足1<m<3且m≤2,解得1<m≤2;
综上,实数m的取值范围是(1,2]∪[3,+∞).
点评 本题考查了一元二次不等式的解的情况和判别式取值的关系,解一元二次不等式,以及复合命题的真假关系的应用问题,是基础题目.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2$\sqrt{2}$-$\frac{1}{2}$,2$\sqrt{2}$-$\frac{1}{2}$) | B. | [-2$\sqrt{2}$-$\frac{1}{2}$,2$\sqrt{2}$-$\frac{1}{2}$] | C. | (-$\sqrt{2}$-$\frac{1}{2}$,$\sqrt{2}$-$\frac{1}{2}$) | D. | [-$\sqrt{2}$-$\frac{1}{2}$,$\sqrt{2}$-$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
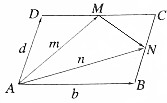 如图所示,平行四边形ABCD中,M为DC的中点,N是BC的中点,设$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,$\overrightarrow{AM}$=$\overrightarrow{m}$,$\overrightarrow{AN}$=$\overrightarrow{n}$.
如图所示,平行四边形ABCD中,M为DC的中点,N是BC的中点,设$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,$\overrightarrow{AM}$=$\overrightarrow{m}$,$\overrightarrow{AN}$=$\overrightarrow{n}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
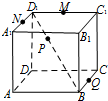 正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在对角线BD1上,给出以下命题:
正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在对角线BD1上,给出以下命题:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③ | C. | ②③ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com