
【题目】已知集合A={x|y= ![]() },B={y|y=x
},B={y|y=x ![]() ,x∈R},C={x|mx<﹣1},
,x∈R},C={x|mx<﹣1},
(1)求R(A∩B);
(2)是否存在实数m使得(A∩B)C成立,若存在,求出m的取值范围;若不存在,请说明理由.
【答案】
(1)解:因为集合A={x|y= ![]() }={x|﹣x2+x+2>0}={x|﹣1<x<2},
}={x|﹣x2+x+2>0}={x|﹣1<x<2},
B={y|y=x ![]() ,x∈R}={y|y∈R}=R,
,x∈R}={y|y∈R}=R,
所以A∩B={x|﹣1<x<2},
所以R(A∩B)={x|x≤﹣1或x≥2}
(2)解:因为A∩B=(﹣1,2),
C={x|mx<﹣1},
假设存在实数m使得(A∩B)C成立,
② 当m=0时,C=,不符合;
②当m>0时,C={x|<﹣ ![]() },
},
于是 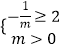 ,无解,不符合;
,无解,不符合;
③当m<0时,C={x|x>﹣ ![]() },
},
于是 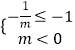 ,无解,不符合;
,无解,不符合;
综上所述,不存在这样的实数m.
【解析】(1)化简集合A、B,再根据交集与补集的定义写出对应的结果;(2)假设存在实数m使得(A∩B)C成立,讨论m=0、m>0和m<0时, 求出集合C,判断是否满足条件即可.
【考点精析】通过灵活运用交、并、补集的混合运算,掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法即可以解答此题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f[g(2)]的值;
(3)求f[g(x)]和g[f(x)]的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 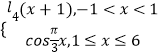 ,若存在实数x1 , x2 , x3 , x4 , 满足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则
,若存在实数x1 , x2 , x3 , x4 , 满足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则 ![]() 的取值范围是( ).
的取值范围是( ).
A.(0,4)
B.(0, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() ,H是BC的中点.
,H是BC的中点. 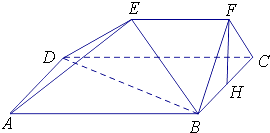
(1)求证:FH∥平面BDE;
(2)求证:AB⊥平面BCF;
(3)求五面体ABCDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD是某小区户外活动空地的平面示意图,其中AB=50![]() 米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
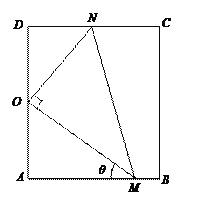
(1)求f(θ)关于θ函数关系式,并写出定义域;
(2)为节约投入成本,当tanθ为何值时,总费用 f(θ)最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点在单位圆上的△ABC中,角A、B、C所对的边分别为a、b、c,且b2+c2=a2+bc.
(1)求角A的大小;
(2)若b2+c2=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),
已知当x∈[0,1]时f(x)=(![]() )1-x,则
)1-x,则
①2是函数f(x)的周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=(![]() )x-3.
)x-3.
其中所有正确命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() (a,b为常数)满足条件
(a,b为常数)满足条件![]() ,且方程
,且方程![]() 有两个相等的实数根.
有两个相等的实数根.
(1)求![]() 的解析式;
的解析式;
(2)是否存在实数![]() (m<n),使得
(m<n),使得![]() 的定义域和值域分别为
的定义域和值域分别为![]() ,如果存在,求出
,如果存在,求出![]() 。不存在,说明理由。
。不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com