
分析 求函数的导数,利用导数研究函数的单调性和最值,建立条件关系进行求解即可.
解答 解:设f(x)=lnx-x+1+a,当x∈[$\frac{1}{e}$,1]时,f′(x)=$\frac{1-x}{x}$>0,f(x)是增函数,
∴x∈[$\frac{1}{e}$,1]时,f(x)∈[a-$\frac{1}{e}$,a],
∵对任意的x1∈[$\frac{1}{e}$,1],总存在x2∈[0,1],使得lnx-x+1+a=x2ex成立,
∴[a-$\frac{1}{e}$,a]是g(x)的不含极值点的单值区间的子集,
∵g′(x)=x(2+x)ex,∴x∈(0,1],g′(x)>0,g(x)=x2ex是增函数,
∴g(x)⊆[0,e]
∴[a-$\frac{1}{e}$,a]⊆[0,e],
∴$\frac{1}{e}$≤a≤e;
故答案为$\frac{1}{e}$≤a≤e.
点评 本题主要考查方程恒成立问题,构造函数,求函数的导数,利用导数研究函数的单调性和取值范围是解决本题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
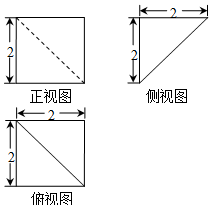
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 30 | 10 |
| 女生 | 20 | 20 |
| P(K2≥k0) | 0.025 | 0.010 |
| k0 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
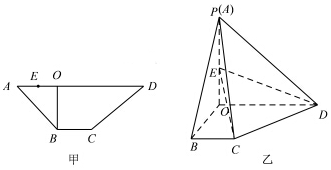
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
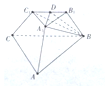 已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6
已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
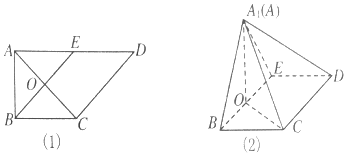
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com