
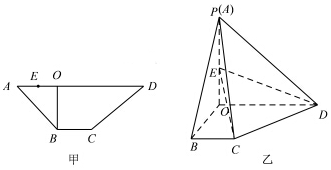
分析 (1)推导出OP⊥OC,OB⊥OP,从而OP⊥平面OPD,以O为原点,建立空间直角坐标系,利用向量法推导出DE和SC不可能垂直.
(2)作出Q点,利用坐标系求出Q的坐标,利用空间距离公式求解即可.
解答 证明:(1)如图甲所示,因为BO是梯形ABCD的高,∠BAD=45°,
所以AO=OB,…(1分)
因为BC=1,OD=2OA,得OD=3,OC=$\sqrt{2}$,…(2分)
如图乙所示,OP=OA=1,OC=$\sqrt{2}$,PC=$\sqrt{3}$,
所以有OP2+OC2=PC2,所以OP⊥OC,…(3分)
而OB⊥OP,OB∩OC=O,所以OP⊥平面OPD,…(4分)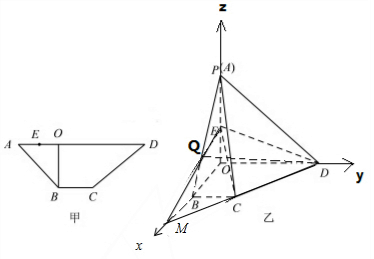
又OB⊥OD,所以OB、OD、OP两两垂直.
故以O为原点,建立空间直角坐标系,如图,
则P(0,0,1),C(1,1,0),D(0,3,0)…(5分)
$\overrightarrow{OP}$=(0,0,1),$\overrightarrow{CD}$=(-1,2,0),
所以$\overrightarrow{OP}•\overrightarrow{CD}$=0,
所以OP⊥CD.…(6分)
解:(2)延长OB,DC,交于点M,连结EM,因为OD=3,BC=1,OB=1,所以BM=$\frac{1}{2}$,…(7分)
EM∩PE=Q,则Q即为平面CDE与PB交点,如图:在平面xoz坐标系中,BP的方程为:x+z=1,ME的方程为:2x+6z=3…(9分),
由$\left\{\begin{array}{l}{x+z=1}\\{2x+6z=3}\end{array}\right.$,解得x=$\frac{3}{4}$,z=$\frac{1}{4}$,在空间直角坐标系中,Q($\frac{3}{4}$,0,$\frac{1}{4}$).
连结DQ,∴|$\overrightarrow{QD}$|=$\sqrt{({\frac{3}{4})}^{2}+{3}^{2}+(\frac{1}{4})^{2}}$=$\frac{\sqrt{154}}{4}$…(12分)
点评 本题考查空间向量的应用,直线与平面垂直的判断与性质定理的应用,空间距离公式的求法,考查转化思想以及计算能力.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:解答题
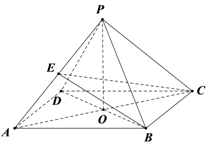 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1009 | B. | -1008 | C. | -1007 | D. | -1006 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com