
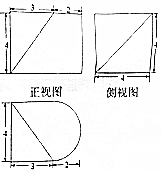
 某几何体的三视图如图所示(其中俯视图中的圆弧是半圆),则该几何体的体积为32+8π.
某几何体的三视图如图所示(其中俯视图中的圆弧是半圆),则该几何体的体积为32+8π.  名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
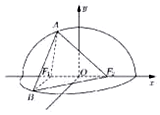 已知椭圆Γ的左、右焦点分别为F1(-1,0)、F2(1,0).经过点F1且倾斜角为θ(0<θ<π)的直线l与椭圆Γ交于A、B两点(其中点A在x轴上方),△ABF2的周长为8.
已知椭圆Γ的左、右焦点分别为F1(-1,0)、F2(1,0).经过点F1且倾斜角为θ(0<θ<π)的直线l与椭圆Γ交于A、B两点(其中点A在x轴上方),△ABF2的周长为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
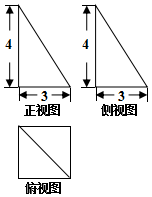
| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
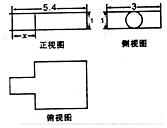 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com