
 两人取到同颜色的球,由甲胜,取到不同颜色的球,则乙胜。
两人取到同颜色的球,由甲胜,取到不同颜色的球,则乙胜。科目:高中数学 来源:不详 题型:解答题
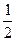 ,且面试是否合格互不影响。求:
,且面试是否合格互不影响。求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,回答第三题正确的概率为
,回答第三题正确的概率为 ,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为
,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为 。
。 的概率分布和数学期望。
的概率分布和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
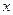 和该年支出维修费用
和该年支出维修费用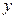 (万元),得到数据如下:
(万元),得到数据如下:使用年限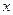 | 2 | 3 | 4 | 5 | 6 |
维修费用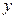 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
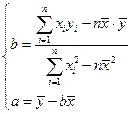 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
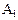 =“第i次抽到红球”,(
=“第i次抽到红球”,(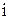 ="1," 2, 3)。试用
="1," 2, 3)。试用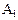 及
及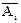 表示下列事件:
表示下列事件:查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.某人投篮3次,投中4次 | B.标准大气压下,水加热到100℃时沸腾 | C.掷一枚质地均匀的硬币,出现“正面朝上” | D.抛掷一颗骰子,出现7点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com