
分析 (Ⅰ)根据绝对值的意义,解方程即可.
(Ⅱ)若不等式f(x)≥g(x)恒成立,利用参数分离法进行转化求函数的最值即可.
(Ⅲ)求出函数G(x)的表达式,讨论对称性的以及a的取值范围进行求解即可.
解答 解:(Ⅰ)若|f(x)|=g(x),
则若|x2-1|=a|x-1|,
即|x-1||x+1|=a|x-1|,
∴x=1或|x+1|=a,
∴a=0或a=2,
(Ⅱ)不等式f(x)≥g(x)恒成立等价为x2-1≥a|x-1|,
①若x=1,则不等式恒成立,
②若x≠1,则a≤($\frac{{x}^{2}-1}{|x-1|}$),
∵y=$\frac{{x}^{2}-1}{|x-1|}$=$\left\{\begin{array}{l}{x+1,}&{x>1}\\{-x-1,}&{x<1}\end{array}\right.$,
∴当x>1时,$\frac{{x}^{2}-1}{|x-1|}$>2,当x<1时,$\frac{{x}^{2}-1}{|x-1|}$>-2,
∴$\frac{{x}^{2}-1}{|x-1|}$>-2,即a≤-2.
(Ⅲ)若a<0时,求G(x)=|f(x)|+g(x)=$\left\{\begin{array}{l}{{x}^{2}-ax+a-1,}&{-2≤x≤-1}\\{-{x}^{2}-ax+a+1,}&{-1<x<1}\\{{x}^{2}+ax-a-1,}&{1≤x≤2}\end{array}\right.$,
①若$\frac{a}{2}$≤-2,即a≤-4,则-$\frac{a}{2}$≥2,
∴G(x)在[-2,-1]上递增,(-1,1)上递增,[1,2]上递减,
∴G(x)max=G(1)=0.
②若-2<$\frac{a}{2}$<-1,即-4<a<-2,则1<-$\frac{a}{2}$<2,
∴G(x)在[-2,$\frac{a}{2}$]上递减,在($\frac{a}{2}$,-1)递增,(-1,1)上递增,(1,-$\frac{a}{2}$)递减,[-$\frac{a}{2}$,2)上递增,
∴G(-2)=3+3a,G(1)=0,G(2)=3+a,
∴当-4<a≤-3时,G(x)max=G(1)=0.
当-3<a<-2时,G(x)max=G(2)=3+a.
③若-1≤$\frac{a}{2}$<0,即-2≤a<0,则0<-$\frac{a}{2}$≤1,
则,G(x)在[-2,-1]上递增,(-1,-$\frac{a}{2}$)上递增,(-$\frac{a}{2}$,1)上递减,[1,2]上递减,
又G(-2)=3+3a,G($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$+a+1,G(2)=3+a,
由于3+a>$\frac{{a}^{2}}{4}$+a+1,
∴G(x)max=G(2)=3+a.
综上,G(x)max$\left\{\begin{array}{l}{0,}&{a≤-3}\\{3+a,}&{-3<a<0}\end{array}\right.$.
点评 本题主要考查不等式恒成立问题,利用参数分离法进行转化求函数的最值,以及利用分类讨论的数学思想是解决本题的关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
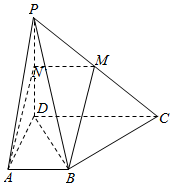 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
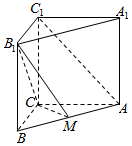 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点M在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点M在线段AB上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{4-2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com