Question

【题目】如图所示，在直角梯形BCEF中，∠CBF=∠BCE=90°，A，D分别是BF，CE上的点，AD∥BC，且AB=DE=2BC=2AF（如图1），将四边形ADEF沿AD折起，连结BE、BF、CE（如图2）．在折起的过程中，下列说法中正确的个数（　　）

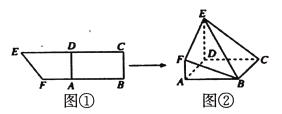
①AC∥平面BEF；

②B、C、E、F四点可能共面；

③若EF⊥CF，则平面ADEF⊥平面ABCD；

④平面BCE与平面BEF可能垂直

A.0B.1C.2D.3

Answer 1

【答案】C

【解析】

根据折叠前后线段、角的变化情况，由线面平行、面面垂直的判定定理和性质定理对各命题进行判断，即可得出答案．

对①，在图②中，连接交于点，取中点，连接MO，易证AOMF为平行四边形，即AC//FM，所以AC//平面BEF，故①正确；

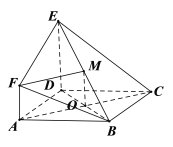
对②，如果B、C、E、F四点共面，则由BC//平面ADEF，可得BC//EF，又AD//BC，所以AD//EF，这样四边形ADEF为平行四边形，与已知矛盾，故②不正确；

对③，在梯形ADEF中，由平面几何知识易得EFFD，又EFCF，∴EF平面CDF，

即有CDEF，∴CD平面ADEF，则平面ADEF平面ABCD，故③正确；

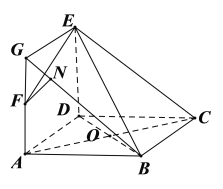
对④，在图②中，延长AF至G，使得AF=FG，连接BG，EG，易得平面BCE平面ABF，BCEG四点共面．过F作FNBG于N，则FN平面BCE，若平面BCE平面BEF，

则过F作直线与平面BCE垂直，其垂足在BE上，矛盾，故④错误．

故选：C．