
【题目】已知首项大于0的等差数列![]() 的公差
的公差![]() ,且
,且![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;
;
①求数列![]() 的通项
的通项![]() ;
;
②是否存在实数![]() ,使得数列
,使得数列![]() 为等比数列?若存在,求出
为等比数列?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
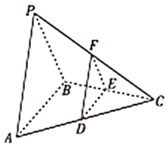
(1)求球![]() 的表面积;
的表面积;
(2)证明:平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() .
.
(3)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列说法中正确的个数( )
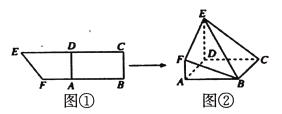
①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足:
满足:![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() .
.
① 记![]() ,求证:数列
,求证:数列![]() 为等差数列;
为等差数列;
② 若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项![]() 应满足的条件.
应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求证:![]() ,并由
,并由![]() 推导
推导![]() 的值;
的值;
(2)若数列![]() 共有
共有![]() 项,前
项,前![]() 项的和为
项的和为![]() ,其后的
,其后的![]() 项的和为
项的和为![]() ,再其后的
,再其后的![]() 项的和为
项的和为![]() ,求
,求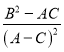 的比值.
的比值.
(3)若数列![]() 的前
的前![]() 项,前
项,前![]() 项、前
项、前![]() 项的和分别为
项的和分别为![]() ,试用含字母
,试用含字母![]() 的式子来表示
的式子来表示![]() (即
(即![]() ,且不含字母
,且不含字母![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节来临之际,某超市为了确定此次春节年货的进货方案,统计去年春节前后50天年货的日销售量(单位:kg),得到如图所示的频率分布直方图.
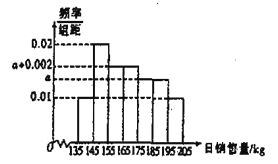
(1)求这50天超市日销售量![]() 的平均数;(视频率为概率,以各组区间的中点值代表该组的值)
的平均数;(视频率为概率,以各组区间的中点值代表该组的值)
(2)先从日销售在![]() ,
,![]() ,
,![]() 内的天数中,按分层抽样随机抽取4天进行比较研究,再从中选2天,求这2天的日销售量都在
内的天数中,按分层抽样随机抽取4天进行比较研究,再从中选2天,求这2天的日销售量都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() :
:![]()
![]() 的左、右焦点,且椭圆
的左、右焦点,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() .点M、N是椭圆
.点M、N是椭圆![]() 上位于
上位于![]() 轴上方的两点,且向量
轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求△
时,求△![]() 的面积;
的面积;
(3)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意
,对于任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对于任意正整数
,求证:对于任意正整数![]() ,都有
,都有![]() ;
;
(3)将数列![]() 、
、![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面”,“当
放在前面”,“当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”得到一个新的数列:
放在前面”的要求进行“交叉排列”得到一个新的数列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 求这个新数列的前
求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com