
【题目】已知函数![]() ,且
,且![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,若对任意的
,若对任意的![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),点
),点![]() 为椭圆短轴的上端点,
为椭圆短轴的上端点,![]() 为椭圆上异于
为椭圆上异于![]() 点的任一点,若
点的任一点,若![]() 点到
点到![]() 点距离的最大值仅在
点距离的最大值仅在![]() 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知
点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知![]() .
.
(1)若![]() ,判断椭圆
,判断椭圆![]() 是否为“圆椭圆”;
是否为“圆椭圆”;
(2)若椭圆![]() 是“圆椭圆”,求
是“圆椭圆”,求![]() 的取值范围;
的取值范围;
(3)若椭圆![]() 是“圆椭圆”,且
是“圆椭圆”,且![]() 取最大值,
取最大值,![]() 为
为![]() 关于原点
关于原点![]() 的对称点,
的对称点,![]() 也异于
也异于![]() 点,直线
点,直线![]() 、
、![]() 分别与
分别与![]() 轴交于
轴交于![]() 、
、![]() 两点,试问以线段
两点,试问以线段![]() 为直径的圆是否过定点?证明你的结论.
为直径的圆是否过定点?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() .
.
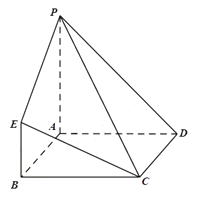
(1)求证:![]() 平面PAD;
平面PAD;
(2)在棱AB上是否存在一点F,使得平面![]() 平面PCE?如果存在,求
平面PCE?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的个数是( )
①直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
②![]() 为异面直线,则过
为异面直线,则过![]() 且与
且与![]() 平行的平面有且仅有一个;
平行的平面有且仅有一个;
③直四棱柱是直平行六面体;
④两相邻侧面所成角相等的棱锥是正棱锥.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列说法中正确的个数( )
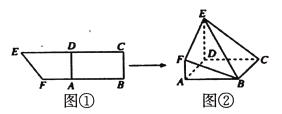
①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求证:![]() ,并由
,并由![]() 推导
推导![]() 的值;
的值;
(2)若数列![]() 共有
共有![]() 项,前
项,前![]() 项的和为
项的和为![]() ,其后的
,其后的![]() 项的和为
项的和为![]() ,再其后的
,再其后的![]() 项的和为
项的和为![]() ,求
,求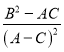 的比值.
的比值.
(3)若数列![]() 的前
的前![]() 项,前
项,前![]() 项、前
项、前![]() 项的和分别为
项的和分别为![]() ,试用含字母
,试用含字母![]() 的式子来表示
的式子来表示![]() (即
(即![]() ,且不含字母
,且不含字母![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com