
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)试判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() ,求
,求![]() 在
在![]() 上的最大值;
上的最大值;
(3)若![]() ,求函数
,求函数![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1)当![]() ,为偶函数,当
,为偶函数,当![]() ,为非奇非偶函数;详见解析
,为非奇非偶函数;详见解析
(2)最大值![]() ;
;
(3) .
.
【解析】
(1)![]() 时,利用定义可以判断
时,利用定义可以判断![]() 为偶函数,
为偶函数,![]() 时,通过反例可判断
时,通过反例可判断![]() 为非奇非偶函数.
为非奇非偶函数.
(2)利用基本不等式和二次函数的性质可求函数的最大值.
(3)由题设可得![]() ,分类讨论求出
,分类讨论求出![]() 在
在![]() 上的最小值后再取两个最小值中的较小者即为
上的最小值后再取两个最小值中的较小者即为![]() 的最小值.
的最小值.
(1)当![]() 时,
时,![]() ,其定义域为
,其定义域为![]() .
.
因为![]() ,故
,故![]() 为偶函数.
为偶函数.
当![]() 时,
时,![]() ,而
,而![]() ,
,
因为![]() ,故
,故![]() ,又
,又![]() ,
,
故![]() 为非奇非偶函数.
为非奇非偶函数.
综上,![]() 时
时![]() 为偶函数,
为偶函数,![]() 时,
时,![]() 为非奇非偶函数.
为非奇非偶函数.
(2)当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() .
.
又![]() ,
,
由基本不等式有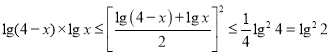 ,
,
当且仅当![]() 时等号成立,故
时等号成立,故![]() 的最大值为
的最大值为![]() .
.
(3)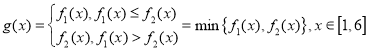 .
.
所以![]() ,其中
,其中![]() .
.
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,因为
时,因为![]() 故
故![]() ;
;
当![]() 时,因为
时,因为![]() 故
故![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
因为![]() ,故
,故![]() .
.
当![]() 时,
时,
当![]() 时,
时,![]() ,
,![]()
此时![]() ,故
,故![]() ,
,![]() ,
,
当![]() 时,由
时,由![]() ,故
,故![]() .
.
当![]() 时,由
时,由![]() ,故
,故![]() .
.
当![]() 时,
时,![]() ,故
,故![]() ,
,![]() ,故
,故![]() .
.
综上, .
.


科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

A.①反映建议(2),③反映建议(1)B.①反映建议(1),③反映建议(2)
C.②反映建议(1),④反映建议(2)D.④反映建议(1),②反映建议(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若
,若![]() (
(![]() 是与
是与![]() 无关的常数,
无关的常数,![]() )则称数列
)则称数列![]() 叫做“弱等差数列”已知数列
叫做“弱等差数列”已知数列![]() 满足:
满足:![]() 且
且![]() ,对于
,对于![]() 恒成立,(其中
恒成立,(其中![]() 都是常数)
都是常数)
(1)求证:数列![]() 是“弱等差数列”,并求出数列
是“弱等差数列”,并求出数列![]() 的通项公式
的通项公式
(2)当![]() 时,若数列
时,若数列![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围
的取值范围
(3)若![]() ,且
,且![]() ,数列
,数列![]() 满足:
满足:![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com