
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间和函数
的单调区间和函数![]() 的最值;
的最值;
(2)已知关于![]() 的不等式
的不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,见解析;(2)![]()
【解析】
(1)求导后,分![]() 和
和![]() 两种情况考虑
两种情况考虑![]() 的单调性;利用导数求
的单调性;利用导数求![]() 的极值即可;
的极值即可;
(2)![]() 对任意的
对任意的![]() 恒成立,等价于
恒成立,等价于![]() 对任意的
对任意的![]() 恒成立,设
恒成立,设![]() ,利用导数研究
,利用导数研究![]() 的单调性以及最值,从而可得到结论.
的单调性以及最值,从而可得到结论.
(1)因为![]() ,∴
,∴![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,![]() 在区间
在区间![]() 上单调递增.
上单调递增.
当![]() ,即
,即![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() ,
,![]() 单调递增;令
单调递增;令![]() ,则
,则![]() ,
,![]() 单调递减.
单调递减.
综上,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;
;
因为![]() ,(
,(![]() )
)
所以![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() ,无最大值.
,无最大值.
(2)![]() 对任意的
对任意的![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,
,![]() ,则
,则![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() 在区间
在区间![]() 上单调递减.所以
上单调递减.所以![]() ,符合题意.
,符合题意.
当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]()
由(1)知![]() ,即
,即![]() 在
在![]() 上恒成立,不符合题意.
上恒成立,不符合题意.
综上,实数![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求证:![]() ,并由
,并由![]() 推导
推导![]() 的值;
的值;
(2)若数列![]() 共有
共有![]() 项,前
项,前![]() 项的和为
项的和为![]() ,其后的
,其后的![]() 项的和为
项的和为![]() ,再其后的
,再其后的![]() 项的和为
项的和为![]() ,求
,求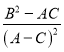 的比值.
的比值.
(3)若数列![]() 的前
的前![]() 项,前
项,前![]() 项、前
项、前![]() 项的和分别为
项的和分别为![]() ,试用含字母
,试用含字母![]() 的式子来表示
的式子来表示![]() (即
(即![]() ,且不含字母
,且不含字母![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义符号函数![]() ,已知函数
,已知函数![]() .
.
(1)已知![]() ,求实数
,求实数![]() 的取值集合;
的取值集合;
(2)当![]() 时,
时,![]() 在区间
在区间![]() 上有唯一零点,求
上有唯一零点,求![]() 的取值集合;
的取值集合;
(3)已知![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求正实数
,求正实数![]() 的取值集合;
的取值集合;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() :
:![]()
![]() 的左、右焦点,且椭圆
的左、右焦点,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() .点M、N是椭圆
.点M、N是椭圆![]() 上位于
上位于![]() 轴上方的两点,且向量
轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求△
时,求△![]() 的面积;
的面积;
(3)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孔子曰:温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系,某校志愿者展开了积极的调查活动:从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查,所得信息如下:
数学成绩优秀(人数) | 数学成绩合格(人数) | |
及时复习(人数) | 20 | 4 |
不及时复习(人数) | 10 | 6 |
(1)张军是640名学生中的一名,他被抽中进行问卷调查的概率是多少(用分数作答);
(2)根据以上数据,运用独立性检验的基本思想,研究数学成绩与及时复习的相关性.
参考公式: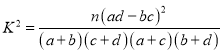 ,其中
,其中![]() 为样本容量
为样本容量
临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点是抛物线
的右焦点是抛物线![]()
![]() 的焦点,直线
的焦点,直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,求
,求![]() 的面积的最小值(
的面积的最小值(![]() 为坐标原点);
为坐标原点);
(3)已知点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com