
【题目】已知椭圆![]() (
(![]() ),点
),点![]() 为椭圆短轴的上端点,
为椭圆短轴的上端点,![]() 为椭圆上异于
为椭圆上异于![]() 点的任一点,若
点的任一点,若![]() 点到
点到![]() 点距离的最大值仅在
点距离的最大值仅在![]() 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知
点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知![]() .
.
(1)若![]() ,判断椭圆
,判断椭圆![]() 是否为“圆椭圆”;
是否为“圆椭圆”;
(2)若椭圆![]() 是“圆椭圆”,求
是“圆椭圆”,求![]() 的取值范围;
的取值范围;
(3)若椭圆![]() 是“圆椭圆”,且
是“圆椭圆”,且![]() 取最大值,
取最大值,![]() 为
为![]() 关于原点
关于原点![]() 的对称点,
的对称点,![]() 也异于
也异于![]() 点,直线
点,直线![]() 、
、![]() 分别与
分别与![]() 轴交于
轴交于![]() 、
、![]() 两点,试问以线段
两点,试问以线段![]() 为直径的圆是否过定点?证明你的结论.
为直径的圆是否过定点?证明你的结论.
【答案】(1)是;(2)![]() ;(3)是,证明见解析.
;(3)是,证明见解析.
【解析】
(1)直接判断即可,
(2)由(1)的方法判断,可得y=﹣2时,函数值达到最大,分别讨论二次项系数的正负,是否满足条件得出a的取值范围;
(3)设参数方程满足以MN为直径的圆过原点,使数量积为零得出定点(0,![]() 2
2![]() ).
).
(1)由题意得椭圆方程:![]() 1,所以A(0,2),
1,所以A(0,2),
设P(x,y)则|PA|2=x2++(y﹣2)2=5(1![]() )+(y﹣2)2
)+(y﹣2)2![]() y2﹣4y+9,y∈[﹣2,2],
y2﹣4y+9,y∈[﹣2,2],
二次函数开口向下,对称轴y=﹣8,y∈[﹣2,2]上函数单调递减,
所以y=﹣2时,函数值最大,此时P为椭圆的短轴的另一个端点,
∴椭圆是“圆椭圆”;
(2)由(1)的方法:椭圆方程:![]() 1,A(0,2)设P(x,y),则|PA|2=x2+(y﹣2)2=a2(1
1,A(0,2)设P(x,y),则|PA|2=x2+(y﹣2)2=a2(1![]() )+(y﹣2)2=(
)+(y﹣2)2=(![]() 1)y2﹣4y+4+a2,y∈[﹣2,2],由题意得,
1)y2﹣4y+4+a2,y∈[﹣2,2],由题意得,
当且仅当y=﹣2时,函数值达到最大,
讨论:①当开口向上时,满足:
![]() ﹣2<a<2(与
﹣2<a<2(与![]() 矛盾,舍);
矛盾,舍);
②当开口向下时,满足 2<a≤2
2<a≤2![]() ,
,
综上a的范围:(2,2![]() ].
].
(3)a=2![]() ,椭圆方程:
,椭圆方程:1,由题意:设P(2
![]() cosθ,sinθ),θ∈[0,2π],且
cosθ,sinθ),θ∈[0,2π],且![]() ,则Q(﹣2
,则Q(﹣2![]() cosθ,﹣sinθ),则直线AP:y
cosθ,﹣sinθ),则直线AP:y![]() x+2M(
x+2M(![]() ,0)
,0)
则直线AQ:y![]() 2N(
2N(![]() ,0),
,0),
MN为直径的圆过定点C,由对称性知C在y轴上,∴设C(0,n)则,且![]() 0,
0,
∴![]() ,
,![]() (
(![]() n),∴
n),∴![]() ,
,
所以得定点(0,![]() 2
2![]() ).
).


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】若存在常数 k(k∈N * , k≥2)、d、t( d , t∈R),使得无穷数列 {a n }满足a n +1 ,则称数列{an }为“段差比数列”,其中常数 k、d、t 分别叫做段长、段差、段比.设数列 {bn }为“段差比数列”.
,则称数列{an }为“段差比数列”,其中常数 k、d、t 分别叫做段长、段差、段比.设数列 {bn }为“段差比数列”.
(1)已知 {bn }的首项、段长、段差、段比分别为1、 2 、 d 、 t .若 {bn }是等比数列,求 d 、 t 的值;
(2)已知 {bn }的首项、段长、段差、段比分别为1、3 、3 、1,其前 3n 项和为 S3n .若不等式 S3n≤ λ 3n1对 n ∈ N *恒成立,求实数 λ 的取值范围;
(3)是否存在首项为 b,段差为 d(d ≠ 0 )的“段差比数列” {bn },对任意正整数 n 都有 bn+6 = bn ,若存在, 写出所有满足条件的 {bn }的段长 k 和段比 t 组成的有序数组 (k, t );若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数)上任意一点
为参数)上任意一点![]() 经过伸缩变换
经过伸缩变换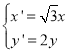 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)长轴的两顶点为A、B,左右焦点分别为F1、F2,焦距为2c且a=2c,过F1且垂直于x轴的直线被椭圆C截得的线段长为3.
(a>b>0)长轴的两顶点为A、B,左右焦点分别为F1、F2,焦距为2c且a=2c,过F1且垂直于x轴的直线被椭圆C截得的线段长为3.
(1)求椭圆C的方程;
(2)在双曲线![]() 上取点Q(异于顶点),直线OQ与椭圆C交于点P,若直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,试证明:k1+k2+k3+k4为定值;
上取点Q(异于顶点),直线OQ与椭圆C交于点P,若直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,试证明:k1+k2+k3+k4为定值;
(3)在椭圆C外的抛物线K:y2=4x上取一点E,若EF1、EF2的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com