
ЁОЬтФПЁПвбжЊЭждВ![]() ЃЈaЃОbЃО0ЃЉГЄжсЕФСНЖЅЕуЮЊAЁЂBЃЌзѓгвНЙЕуЗжБ№ЮЊF1ЁЂF2ЃЌНЙОрЮЊ2cЧвa=2cЃЌЙ§F1ЧвДЙжБгкxжсЕФжБЯпБЛЭждВCНиЕУЕФЯпЖЮГЄЮЊ3ЃЎ
ЃЈaЃОbЃО0ЃЉГЄжсЕФСНЖЅЕуЮЊAЁЂBЃЌзѓгвНЙЕуЗжБ№ЮЊF1ЁЂF2ЃЌНЙОрЮЊ2cЧвa=2cЃЌЙ§F1ЧвДЙжБгкxжсЕФжБЯпБЛЭждВCНиЕУЕФЯпЖЮГЄЮЊ3ЃЎ
ЃЈ1ЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈ2ЃЉдкЫЋЧњЯп![]() ЩЯШЁЕуQЃЈвьгкЖЅЕуЃЉЃЌжБЯпOQгыЭждВCНЛгкЕуPЃЌШєжБЯпAPЁЂBPЁЂAQЁЂBQЕФаБТЪЗжБ№ЮЊk1ЁЂk2ЁЂk3ЁЂk4ЃЌЪджЄУїЃКk1+k2+k3+k4ЮЊЖЈжЕЃЛ
ЩЯШЁЕуQЃЈвьгкЖЅЕуЃЉЃЌжБЯпOQгыЭждВCНЛгкЕуPЃЌШєжБЯпAPЁЂBPЁЂAQЁЂBQЕФаБТЪЗжБ№ЮЊk1ЁЂk2ЁЂk3ЁЂk4ЃЌЪджЄУїЃКk1+k2+k3+k4ЮЊЖЈжЕЃЛ
ЃЈ3ЃЉдкЭждВCЭтЕФХзЮяЯпKЃКy2=4xЩЯШЁвЛЕуEЃЌШєEF1ЁЂEF2ЕФаБТЪЗжБ№ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ0ЃЈ3ЃЉ
ЃЈ2ЃЉ0ЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЭждВЕФЭЈОЖЙЋЪНМАa=2cЃЌМДПЩЧѓЕУaКЭbЕФжЕЃЌМДПЩЧѓЕУЭждВЗНГЬЗНГЬЃЛ
ЃЈ2ЃЉИљОнжБЯпЕФаБТЪЙЋЪНЃЌЧѓЕУ![]() ЃЌ
ЃЌ ![]() ЃЌгЩ
ЃЌгЩ![]() ЙВЯпЃЌЕУ
ЙВЯпЃЌЕУ![]()
![]() ЃЌМДПЩЧѓЕУНсТлЃЛ
ЃЌМДПЩЧѓЕУНсТлЃЛ
ЃЈ3ЃЉЯШгУEЕузјБъБэЪО![]() ЃЌдйИљОнКЏЪ§ЕЅЕїадМДПЩЧѓЕУ
ЃЌдйИљОнКЏЪ§ЕЅЕїадМДПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉгЩЬтвтa=2cЃЌЭждВЕФЭЈОЖЮЊ![]() =3ЃЌ
=3ЃЌ
вђЮЊa2=b2+c2ЃЌЫљвдa=2ЃЌb=![]() ЃЌc=1ЃЌ
ЃЌc=1ЃЌ
ЁрЭждВЕФБъзМЗНГЬЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЃКAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌF1ЃЈЉ1ЃЌ0ЃЉЃЌF2ЃЈ1ЃЌ0ЃЉЃЌЩшPЃЈx1ЃЌy1ЃЉЃЌ
дђ![]() ЃЌдђ
ЃЌдђ![]()
![]() =
=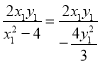
![]()
![]()
ЩшQЃЈx2ЃЌy2ЃЉЃЌдђ![]() ЃЌдђ
ЃЌдђ
дђ![]()
![]() =
=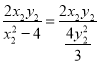 =
=![]() ЃЌ
ЃЌ
гж![]() ЙВЯпЃЌЁр
ЙВЯпЃЌЁр![]() ЃЌ
ЃЌ![]()
ЃЈ3ЃЉЩш![]() ЃЌгЩ
ЃЌгЩ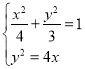 ЃЌНтЕУЃК
ЃЌНтЕУЃК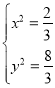 ЃЌ
ЃЌ
гЩEдкЭждВCЭтЕФХзЮяЯпKЃКy2=4xЩЯвЛЕуЃЌдђ![]() ЃЌ
ЃЌ
дђEF1 ЁЂEF2ЕФаБТЪЗжБ№ЮЊ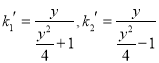 ЃЌЃЈ
ЃЌЃЈ![]() ЃЉ
ЃЉ![]()
дђ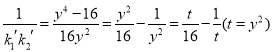 ЃЌЃЈ
ЃЌЃЈ![]() ЃЉ
ЃЉ
дкЃЈ![]() ЃЌ4ЃЉЃЌЃЈ4ЃЌ+ЁоЃЉЩЯЗжБ№ЕЅЕїЕндіЃЌ
ЃЌ4ЃЉЃЌЃЈ4ЃЌ+ЁоЃЉЩЯЗжБ№ЕЅЕїЕндіЃЌ
Ёр![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ![]() ЃЎ
ЃЎ


 ЪБПЬзМБИзХЪюМйзївЕдзгФмГіАцЩчЯЕСаД№АИ
ЪБПЬзМБИзХЪюМйзївЕдзгФмГіАцЩчЯЕСаД№АИ ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ МйЦкзївЕЪюМйГЩГЄРждАаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
МйЦкзївЕЪюМйГЩГЄРждАаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫМьВтФГжжСуМўЕФвЛЬѕЩњВњЯпЕФЩњВњЙ§ГЬЃЌДгЩњВњЯпЩЯЫцЛњГщШЁвЛХњСуМўЃЌИљОнЦфГпДчЕФЪ§ОнЗжГЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() зщЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.ШєГпДчТфдкЧјМф
зщЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.ШєГпДчТфдкЧјМф![]() жЎЭтЃЌдђШЯЮЊИУСуМўЪєЁАВЛКЯИёЁБЕФСуМўЃЌЦфжа
жЎЭтЃЌдђШЯЮЊИУСуМўЪєЁАВЛКЯИёЁБЕФСуМўЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊбљБОЦНОљКЭбљБОБъзМВюЃЌМЦЫуПЩЕУ
ЗжБ№ЮЊбљБОЦНОљКЭбљБОБъзМВюЃЌМЦЫуПЩЕУ![]() ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉ.
ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉ.
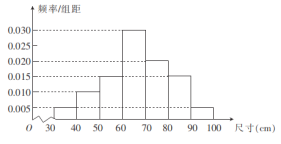
ЃЈ1ЃЉШєвЛИіСуМўЕФГпДчЪЧ![]() ЃЌЪдХаЖЯИУСуМўЪЧЗёЪєгкЁАВЛКЯИёЁБЕФСуМўЃЛ
ЃЌЪдХаЖЯИУСуМўЪЧЗёЪєгкЁАВЛКЯИёЁБЕФСуМўЃЛ
ЃЈ2ЃЉЙЄГЇРћгУЗжВуГщбљЕФЗНЗЈДгбљБОЕФЧА![]() зщжаГщГі
зщжаГщГі![]() ИіСуМўЃЌБъЩЯМЧКХЃЌВЂДгет
ИіСуМўЃЌБъЩЯМЧКХЃЌВЂДгет![]() ИіСуМўжадйГщШЁ
ИіСуМўжадйГщШЁ![]() ИіЃЌЧѓдйДЮГщШЁЕФ
ИіЃЌЧѓдйДЮГщШЁЕФ![]() ИіСуМўжаЧЁга
ИіСуМўжаЧЁга![]() ИіГпДчаЁгк
ИіГпДчаЁгк![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃЈ
ЃЈ![]() ЃЉЃЌЕу
ЃЉЃЌЕу![]() ЮЊЭждВЖЬжсЕФЩЯЖЫЕуЃЌ
ЮЊЭждВЖЬжсЕФЩЯЖЫЕуЃЌ![]() ЮЊЭждВЩЯвьгк
ЮЊЭждВЩЯвьгк![]() ЕуЕФШЮвЛЕуЃЌШє
ЕуЕФШЮвЛЕуЃЌШє![]() ЕуЕН
ЕуЕН![]() ЕуОрРыЕФзюДѓжЕНідк
ЕуОрРыЕФзюДѓжЕНідк![]() ЕуЮЊЖЬжсЕФСэвЛЖЫЕуЪБШЁЕНЃЌдђГЦДЫЭждВЮЊЁАдВЭждВЁБЃЌвбжЊ
ЕуЮЊЖЬжсЕФСэвЛЖЫЕуЪБШЁЕНЃЌдђГЦДЫЭждВЮЊЁАдВЭждВЁБЃЌвбжЊ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌХаЖЯЭждВ
ЃЌХаЖЯЭждВ![]() ЪЧЗёЮЊЁАдВЭждВЁБЃЛ
ЪЧЗёЮЊЁАдВЭждВЁБЃЛ
ЃЈ2ЃЉШєЭждВ![]() ЪЧЁАдВЭждВЁБЃЌЧѓ
ЪЧЁАдВЭждВЁБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєЭждВ![]() ЪЧЁАдВЭждВЁБЃЌЧв
ЪЧЁАдВЭждВЁБЃЌЧв![]() ШЁзюДѓжЕЃЌ
ШЁзюДѓжЕЃЌ![]() ЮЊ
ЮЊ![]() ЙигкдЕу
ЙигкдЕу![]() ЕФЖдГЦЕуЃЌ
ЕФЖдГЦЕуЃЌ![]() вВвьгк
вВвьгк![]() ЕуЃЌжБЯп
ЕуЃЌжБЯп![]() ЁЂ
ЁЂ![]() ЗжБ№гы
ЗжБ№гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЪдЮЪвдЯпЖЮ
СНЕуЃЌЪдЮЪвдЯпЖЮ![]() ЮЊжБОЖЕФдВЪЧЗёЙ§ЖЈЕуЃПжЄУїФуЕФНсТл.
ЮЊжБОЖЕФдВЪЧЗёЙ§ЖЈЕуЃПжЄУїФуЕФНсТл.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉаДГіЧњЯп![]() ЕФМЋзјБъЗНГЬЃЌВЂЧѓГіЧњЯп
ЕФМЋзјБъЗНГЬЃЌВЂЧѓГіЧњЯп![]() гы
гы![]() ЙЋЙВЯвЫљдкжБЯпЕФМЋзјБъЗНГЬЃЛ
ЙЋЙВЯвЫљдкжБЯпЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєЩфЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌгыЧњЯп
СНЕуЃЌгыЧњЯп![]() НЛгк
НЛгк![]() ЕуЃЌЧв
ЕуЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшШ§РтзЖ![]() ЕФУПИіЖЅЕуЖМдкЧђ
ЕФУПИіЖЅЕуЖМдкЧђ![]() ЕФЧђУцЩЯЃЌ
ЕФЧђУцЩЯЃЌ![]() ЪЧУцЛ§ЮЊ
ЪЧУцЛ§ЮЊ![]() ЕФЕШБпШ§НЧаЮЃЌ
ЕФЕШБпШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧвЦНУц
ЃЌЧвЦНУц![]() ЦНУц
ЦНУц![]() .
.
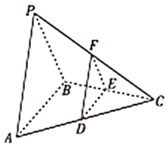
ЃЈ1ЃЉЧѓЧђ![]() ЕФБэУцЛ§ЃЛ
ЕФБэУцЛ§ЃЛ
ЃЈ2ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЧвЦНУц
ЃЌЧвЦНУц![]() ЦНУц
ЦНУц![]() .
.
ЃЈ3ЃЉгыВрУц![]() ЦНааЕФЦНУц
ЦНааЕФЦНУц![]() гыРт
гыРт![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№НЛгк
ЗжБ№НЛгк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФУцЬх
ЃЌЧѓЫФУцЬх![]() ЕФЬхЛ§ЕФзюДѓжЕ.
ЕФЬхЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉЬжТлКЏЪ§![]() СуЕуЕФИіЪ§ЃЛ
СуЕуЕФИіЪ§ЃЛ
ЃЈ3ЃЉШє![]() ДцдкСНИіВЛЭЌЕФСуЕу
ДцдкСНИіВЛЭЌЕФСуЕу![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФМИКЮЬхжаЃЌЫФБпаЮABCDЮЊе§ЗНаЮЃЌ![]() ЦНУцABCDЃЌ
ЦНУцABCDЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
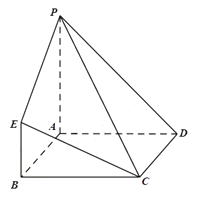
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУцPADЃЛ
ЦНУцPADЃЛ
ЃЈ2ЃЉдкРтABЩЯЪЧЗёДцдквЛЕуFЃЌЪЙЕУЦНУц![]() ЦНУцPCEЃПШчЙћДцдкЃЌЧѓ
ЦНУцPCEЃПШчЙћДцдкЃЌЧѓ![]() ЕФжЕЃЛШчЙћВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШчЙћВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШВюЪ§Са![]() ЕФЪзЯюЮЊ
ЕФЪзЯюЮЊ![]() ЃЌЙЋВюЮЊ
ЃЌЙЋВюЮЊ![]() ЃЌЕШБШЪ§Са
ЃЌЕШБШЪ§Са![]() ЕФЪзЯюЮЊ
ЕФЪзЯюЮЊ![]() ЃЌЙЋБШЮЊ
ЃЌЙЋБШЮЊ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЌВЂгЩ
ЃЌВЂгЩ![]() ЭЦЕМ
ЭЦЕМ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєЪ§Са![]() ЙВга
ЙВга![]() ЯюЃЌЧА
ЯюЃЌЧА![]() ЯюЕФКЭЮЊ
ЯюЕФКЭЮЊ![]() ЃЌЦфКѓЕФ
ЃЌЦфКѓЕФ![]() ЯюЕФКЭЮЊ
ЯюЕФКЭЮЊ![]() ЃЌдйЦфКѓЕФ
ЃЌдйЦфКѓЕФ![]() ЯюЕФКЭЮЊ
ЯюЕФКЭЮЊ![]() ЃЌЧѓ
ЃЌЧѓ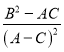 ЕФБШжЕЃЎ
ЕФБШжЕЃЎ
ЃЈ3ЃЉШєЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюЃЌЧА
ЯюЃЌЧА![]() ЯюЁЂЧА
ЯюЁЂЧА![]() ЯюЕФКЭЗжБ№ЮЊ
ЯюЕФКЭЗжБ№ЮЊ![]() ЃЌЪдгУКЌзжФИ
ЃЌЪдгУКЌзжФИ![]() ЕФЪНзгРДБэЪО
ЕФЪНзгРДБэЪО![]() ЃЈМД
ЃЈМД![]() ЃЌЧвВЛКЌзжФИ
ЃЌЧвВЛКЌзжФИ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com