
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程,并求出曲线
的极坐标方程,并求出曲线![]() 与
与![]() 公共弦所在直线的极坐标方程;
公共弦所在直线的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 点,且
点,且![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
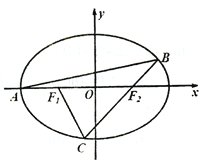
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月16日,公安部联合阿里巴巴推出的“钱盾反诈机器人”正式上线,当普通民众接到电信网络诈骗电话,公安部钱盾反诈预警系统预警到这一信息后,钱盾反诈机器人即自动拨打潜在受害人的电话予以提醒,来电信息显示为“公安反诈专号”.某法制自媒体通过自媒体调查民众对这一信息的了解程度,从5000多参与调查者中随机抽取200个样本进行统计,得到如下数据:男性不了解这一信息的有50人,了解这一信息的有80人,女性了解这一信息的有40人.
(1)完成下列![]() 列联表,问:能否在犯错误的概率不超过0.01的前提下,认为200个参与调查者是否了解这一信息与性别有关?
列联表,问:能否在犯错误的概率不超过0.01的前提下,认为200个参与调查者是否了解这一信息与性别有关?
了解 | 不了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(2)该自媒体对200个样本中了解这一信息的调查者按照性别分组,用分层抽样的方法抽取6人,再从这6人中随机抽取3人给予一等奖,另外3人给予二等奖,求一等奖与二等奖获得者都有女性的概率.
附:![]()
P(K2≥k) | 0.01 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆C满足:圆心在
中,已知圆C满足:圆心在![]() 轴上,且与圆
轴上,且与圆![]() 相外切.设圆C与
相外切.设圆C与![]() 轴的交点为M,N,若圆心C在
轴的交点为M,N,若圆心C在![]() 轴上运动时,在
轴上运动时,在![]() 轴正半轴上总存在定点
轴正半轴上总存在定点![]() ,使得
,使得![]() 为定值,则点
为定值,则点![]() 的纵坐标为_________.
的纵坐标为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区是一个以![]() 为圆心,半径为
为圆心,半径为![]() 的圆形区域,道路
的圆形区域,道路![]() ,
,![]() 成
成![]() 角,且均和景区边界相切,现要修一条与景区相切的观光木栈道
角,且均和景区边界相切,现要修一条与景区相切的观光木栈道![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上,修建的木栈道
上,修建的木栈道![]() 与道路
与道路![]() ,
,![]() 围成的三角地块
围成的三角地块![]() .
.

(1)求修建的木栈道![]() 与道路
与道路![]() ,
,![]() 围成的三角地块
围成的三角地块![]() 面积的最小值;
面积的最小值;
(2)若景区中心![]() 与木栈道
与木栈道![]() 段连线的
段连线的![]() .
.
①将木栈道![]() 的长度表示为
的长度表示为![]() 的函数,并指定定义域;
的函数,并指定定义域;
②求出木栈道![]() 的长度最小值.
的长度最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义域为R的周期函数,最小正周期为2,且
f(1+x)=f(1-x),当-1≤x≤0时,f(x)=-x.
(1)判断f(x)的奇偶性;
(2)试求出函数f(x)在区间[-1,2]上的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com