
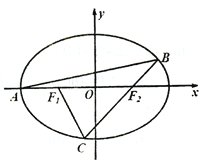
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2) (3)
(3)![]()
【解析】试题分析:
(1)由题意得到关于![]() 的方程组,求解方程组可得椭圆
的方程组,求解方程组可得椭圆![]() 的标准方程:
的标准方程: ![]() ;
;
(2)由题意可得点![]() 在
在![]() 轴下方据此分类讨论有:
轴下方据此分类讨论有: ![]() ,联立直线
,联立直线![]() 的方程与椭圆方程可得
的方程与椭圆方程可得 ;
;
(3)设直线![]() 的方程
的方程![]() ,联立直线方程与椭圆方程,可得
,联立直线方程与椭圆方程,可得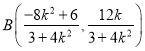 利用几何关系
利用几何关系![]() 计算可得
计算可得![]() ,利用点
,利用点![]() 在椭圆上得到关于实数k的方程,解方程有:
在椭圆上得到关于实数k的方程,解方程有: ![]() .
.
试题解析:
(1)由题意得 ,解得
,解得
∴椭圆![]() 的标准方程:
的标准方程: ![]()
(2)∵![]() 为等腰三角形,且
为等腰三角形,且![]() ∴点
∴点![]() 在
在![]() 轴下方
轴下方
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则
,则![]() ,∴
,∴![]() ;
;
![]() 若
若![]() ,则
,则![]() ,∴
,∴![]() ;
;
∴![]()
∴直线![]() 的方程
的方程![]() ,由
,由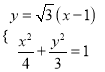 得
得 或
或
∴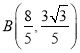
(3)设直线![]() 的方程
的方程![]() ,
,
由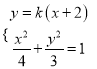 得
得![]()
∴![]() ∴
∴![]()
∴![]() ∴
∴
若![]() ,则∴
,则∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() 与
与![]() 不垂直;
不垂直;
∴![]() ,∵
,∵![]() ,
, ![]() ,
,
∴直线![]() 的方程
的方程![]() ,直线
,直线![]() 的方程:
的方程: ![]()
由 解得
解得![]() ∴
∴![]()
又点![]() 在椭圆上得
在椭圆上得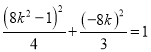 ,即
,即![]() ,即
,即![]()
∵![]() ,∴
,∴![]()


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家商场销售一种商品,该商品一天的需求量在![]() 范围内等可能取值,该商品的进货量也在
范围内等可能取值,该商品的进货量也在![]() 范围内取值(每天进货1次).这家商场每销售一件该商品可获利60元;若供不应求,可从其他商店调拨,销售一件该商品可获利40元;若供大于求,剩余的每处理一件该商品亏损20元.设该商品每天的需求量为
范围内取值(每天进货1次).这家商场每销售一件该商品可获利60元;若供不应求,可从其他商店调拨,销售一件该商品可获利40元;若供大于求,剩余的每处理一件该商品亏损20元.设该商品每天的需求量为![]() ,每天的进货量为
,每天的进货量为![]() 件,该商场销售该商品的日利润为
件,该商场销售该商品的日利润为![]() 元.
元.
(1)写出这家商场销售该商品的日利润为![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)写出供大于求,销售![]() 件商品时,日利润
件商品时,日利润![]() 的分布列;
的分布列;
(3)当进货量![]() 多大时,该商场销售该商品的日利润的期望值最大?并求出日利润的期望值的最大值.
多大时,该商场销售该商品的日利润的期望值最大?并求出日利润的期望值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,沿直线
中点,沿直线![]() 将
将![]() 翻折成
翻折成![]() ,使平面
,使平面![]() 平面
平面![]() .点
.点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,使
向上翻折,使![]() 与
与![]() 重合,则
重合,则![]() __________,四棱锥
__________,四棱锥![]() 的体积为__________.
的体积为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程,并求出曲线
的极坐标方程,并求出曲线![]() 与
与![]() 公共弦所在直线的极坐标方程;
公共弦所在直线的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 点,且
点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com