
����Ŀ��2016��6��22 �գ������ʽ�����Ϣ����ᡱ��ɽ���ൺ��Ļ.Ϊ�˽���Щ�˸���ע�����ʽ�����Ϣ����ᡱ��ij���������ȡ��������15-75��֮���100�˽��е��飬����������Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�����������Ϊ�� ![]() .��������������
.��������������![]() ��
��![]() �ڵ��˷ֱ��Ϊ �������ꡱ�͡������ꡱ.
�ڵ��˷ֱ��Ϊ �������ꡱ�͡������ꡱ.
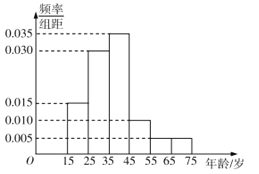
��1������Ƶ�ʷֲ�ֱ��ͼ����������λ����������λС������������
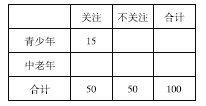
��2��������֪������������![]() ������,���ж��ܷ���
������,���ж��ܷ���![]() �İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ��
�İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ��
��:�ο���ʽ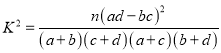 ������
������![]() .
.
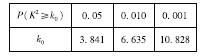
�ٽ�ֵ����
���𰸡���1��36.43����2����![]() �İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ
�İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ
�������������������1������Ƶ�ʷֲ�ֱ��ͼ��֪����������Ϊ40����Ϊ![]() ��
��
����������λ��Ϊ![]() ����
����![]() ������
������![]() ������������λ��ԼΪ36.43.��2���ֱ���á��������ˡ������������ˡ����������2��2����������K2�����ٽ�ֵ�Աȣ����ɵõ���99%�İ�����Ϊ���������ˡ��ȡ��������ˡ����ӹ�ע���ᣮ
������������λ��ԼΪ36.43.��2���ֱ���á��������ˡ������������ˡ����������2��2����������K2�����ٽ�ֵ�Աȣ����ɵõ���99%�İ�����Ϊ���������ˡ��ȡ��������ˡ����ӹ�ע���ᣮ
���������
��1������Ƶ�ʷֲ�ֱ��ͼ��֪����������Ϊ40����Ϊ![]() ��
��
����������λ��Ϊ![]() ����
����![]() ������
������![]() ������������λ��ԼΪ36.43.
������������λ��ԼΪ36.43.
��2���������֪����ȡ�ġ������ꡱ����![]() �ˣ��������ꡱ����
�ˣ��������ꡱ����![]() ��.
��.
��ɵ�![]() ���������£�
���������£�

��������������ݵ�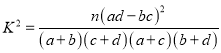
![]() ��
��
��Ϊ![]() ,
,
������![]() �İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ.
�İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��б������A1B1C1��ABC�У�����AA1C1C�͵���ABC������AA1C1C�����Σ���A1AC=60�㣬AC=3��AB=BC=2��E��F�ֱ���A1C1 �� AB���е㣮 
��1����֤��EF��ƽ��BB1C1C��
��2����֤��CE����ABC��
��3��������E��BCC1B1�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ��� ��
A. ���⡰��![]() ����
����![]() ���ķ�����Ϊ����
���ķ�����Ϊ����![]() ����
����![]() ��
��
B. ���⡰����![]() ��ʹ��
��ʹ��![]() ���ķ���:������
���ķ���:������![]() ������
������![]() ��
��
C. �����⡰��![]() �������⡰
�������⡰![]() ��
��![]() �����������⣬��ô����
�����������⣬��ô����![]() һ����������
һ����������
D. ���⡰��![]() ����
����![]() ������������������
������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ڵȲ�����![]() �У���֪
�У���֪![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ����
����![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ȡ�����ֵ��������������ֵ��
ȡ�����ֵ��������������ֵ��
��2����֪����![]() ��ͨ�ʽ��
��ͨ�ʽ��![]() ��������
��������![]() ��ǰ
��ǰ![]() ���.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() �����Ҷ���ֱ�Ϊ
�����Ҷ���ֱ�Ϊ![]() ���ϡ��¶���ֱ�Ϊ
���ϡ��¶���ֱ�Ϊ![]() ����������ֱ�Ϊ
����������ֱ�Ϊ![]() ��
�� ![]() ���ı���
���ı���![]() ��������ı���
��������ı���![]() �������2��.
�������2��.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������Բ![]() ���ҽ����Ҵ�ֱ��
���ҽ����Ҵ�ֱ��![]() ���ֱ�߽���Բ
���ֱ�߽���Բ![]() ��
��![]() ���㣬
���㣬 ![]() ����Բ
����Բ![]() ��λ��ֱ��
��λ��ֱ��![]() ���������.��
���������.��![]() ����֤��ֱ��
����֤��ֱ��![]() ��б��
��б��![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ�����Σ�PD��ƽ��ABCD��PD��QA��QA=AB= ![]() PD��
PD�� 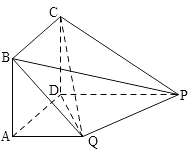
��1��֤����ƽ��PQC��ƽ��DCQ
��2��������Q��BP��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪cos��= ![]() ��cos����+�£�=��
��cos����+�£�=�� ![]() ���Ҧ����¡ʣ�0��
���Ҧ����¡ʣ�0�� ![]() ������cos�������£���ֵ���ڣ� ��
������cos�������£���ֵ���ڣ� ��
A.�� ![]()
B.![]()
C.�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() .��
.��![]() ����Բ
����Բ![]() �ϣ�ֱ��
�ϣ�ֱ��![]() ������ԭ��
������ԭ��![]() ����
����![]() ��
�� ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�� ����Բ�ڵ�![]() ��������Ϊֱ��
��������Ϊֱ��![]() ����
����![]() ��
��![]() �ϵ���Ӱ�ֱ�Ϊ
�ϵ���Ӱ�ֱ�Ϊ![]() ����
����![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ���ڵ�
���ڵ�![]() ������
������![]() �Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵������.
�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��ABCD���������ⳤ��ȣ�����ABCDΪ�����Σ�MΪPB���е㣬��֤��
����PD��ƽ��ACM��
����PO��ƽ��ABCD��
������PA=AB��������ֱ��PD��CM���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com