Question

【题目】已知函数

（1）当时，求函数的图象在处的切线方程；

（2）若函数在定义域上为单调增函数。

①求的最大整数值；

②证明：

Answer 1

【答案】(1) .

(2) ①2；②证明见解析.

【解析】分析：（1）当时，化简函数的解析式，求出函数的导数，求出斜率，然后利用点斜式求函数的图象在处的切线方程；（2）①函数在定义域上为单调增函数，则恒成立.先证明，设，则，推出

当时，恒成立，当时，，即不恒成立，可得的最大整数值为；②由①知，，令，由此可知，当时，，当时，；当时，.....；当时，，即可得出结论.

详解：（1）当时，

∴

又，

所以

所求切线方程为，即

（2）由题意知，

若函数在定义域上为单调增函数，则恒成立，

①先证明，设，则

则函数在单调递减，在单调递增

所以，即

同理可证，

所以，

所以

当时，恒成立，

当时，，即不恒成立

综上所述，的最大整数值为

②由①知，，令

所以，

所以

由此可知，当时，

当时，

当时，.....，

当时，

累加得

又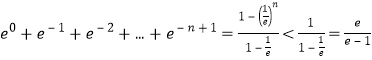

所以

即