
【题目】某网站登录密码由四位数字组成,某同学将四个数字0,3,2,5,编排了一个顺序作为密码.由于长时间未登录该网站,他忘记了密码.若登录时随机输入由0,3,2,5组成的一个密码,则该同学不能顺利登录的概率是多少?
【答案】![]()
【解析】
利用间接法求概率,利用树状图获得样本点的个数,进而先求得“输入由0,3,2,5组成的一个四位数字,恰是密码”的概率,根据对立事件获得所求即可
用事件A表示“输入由0,3,2,5组成的一个四位数字,但不是密码”,由于事件A比较复杂,可考虑它的对立事件![]() ,即“输入由0,3,2,5组成的一个四位数字,恰是密码”,
,即“输入由0,3,2,5组成的一个四位数字,恰是密码”,
显然它只有一种结果,
四个数字0,3,2,5随机编排顺序,所有可能结果可用树状图表示,如图,




从树状图可以看出,将四个数字0,3,2,5随机编排顺序,共有24种可能的结果,即样本空间共含有24个样本点,且24个样本点出现的结果是等可能的,因此可以用古典概型来解决,由![]() ,得
,得![]() ,
,
因此,随机输入由0,3,2,5组成的一个24四位数字,但不是密码,即该同学不能顺利登录的概率为![]()


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】某育种基地对某个品种的种子进行试种观察,经过一个生长期培养后,随机抽取![]() 株作为样本进行研究。株高在
株作为样本进行研究。株高在![]() 及以下为不良,株高在
及以下为不良,株高在![]() 到
到![]() 之间为正常,株高在
之间为正常,株高在![]() 及以上为优等。下面是这
及以上为优等。下面是这![]() 个样本株高指标的茎叶图和频率分布直方图,但是由于数据递送过程出现差错,造成图表损毁。请根据可见部分,解答下面的问题:
个样本株高指标的茎叶图和频率分布直方图,但是由于数据递送过程出现差错,造成图表损毁。请根据可见部分,解答下面的问题:

(1)求![]() 的值并在答题卡的附图中补全频率分布直方图;
的值并在答题卡的附图中补全频率分布直方图;
(2)通过频率分布直方图估计这![]() 株株高的中位数(结果保留整数);
株株高的中位数(结果保留整数);
(3)从育种基地内这种品种的种株中随机抽取2株,记![]() 表示抽到优等的株数,由样本的频率作为总体的概率,求随机变量
表示抽到优等的株数,由样本的频率作为总体的概率,求随机变量![]() 的分布列(用最简分数表示).
的分布列(用最简分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点,![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 、
、![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得点
,使得点![]() 平分线段
平分线段![]() ,
,![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假.
(1)若直线![]() 上有无数个点不在平面
上有无数个点不在平面![]() 内,则
内,则![]() ;
;
(2)若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都平行;
内的任意一条直线都平行;
(3)若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都没有公共点;
内的任意一条直线都没有公共点;
(4)如果两条平行直线中的一条与一个平面平行,则另一条直线也与这个平面平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知线C的极坐标方程为:ρ=2![]() sin(θ+
sin(θ+![]() ),过P(0,1)的直线l的参数方程为:
),过P(0,1)的直线l的参数方程为: (t为参数),直线l与曲线C交于M,N两点.
(t为参数),直线l与曲线C交于M,N两点.
(1)求出直线l与曲线C的直角坐标方程.
(2)求|PM|2+|PN|2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A. 函数![]() 的一条对称轴是
的一条对称轴是![]()
B. 函数![]() 的一个对称中心是
的一个对称中心是![]()
C. 函数![]() 的一条对称轴是
的一条对称轴是![]()
D. 函数![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂推出品牌为“玉兔”的新产品,生产“玉兔”的固定成本为20000元,每生产一件“玉兔”需要增加投入100元,根据统计数据,总收益P(单位:元)与月产量x(单位:件)满足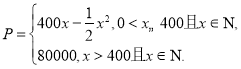 (注:总收益=总成本+利润)
(注:总收益=总成本+利润)
(1)请将利润y(单位:元)表示成关于月产量x(单位:件)的函数;
(2)当月产量为多少时,利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com