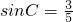Question

若A，B，C是△ABC的三个内角，，．求cosA的值．

Answer 1

解：∵cosB=，∴sinB=，
又sinC=，cosC=±，
若cosC=-，则角C是钝角，角B为锐角，π-C为锐角，而sin（π-C）=，
sinB=，于是 sin（π-C）＜sinB，
∴B＞π-C，B+C＞π，矛盾，
∴cosC≠-，cosC=，
∵A+B+C=π
∴cosA=-cos（B+C）
=-（cosBcosC-sinBsinC）=-（×-×）=．
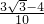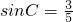分析：由，，利用同角三角函数间的基本关系分别求出sinB和cosC的值，得到cosC的值有两解，假如cosC的解为负数得到C为钝角，则B和π-C为锐角，然后根据sinB和sin（π-C）的值，利用正弦函数的单调性得到B大于π-C，即B+C大于π，与三角形的内角和定理矛盾，所以假设错误，cosC只能等于正值，把所求的式子cosA利用诱导公式化简后，得到cosA等于-cos（B+C），然后利用两角和的余弦函数公式化简后，将各自的值代入即可求出原式的值．
点评：此题考查学生灵活运用同角三角函数间的基本关系、诱导公式及两角和的余弦函数公式化简求值，是一道综合题．