
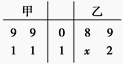
【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
【答案】(1)甲组成绩比乙组稳定 (2)![]()
【解析】试题分析:(1)根据两组数据的平均数相等,可得x的值,进而求出两组数据的方差,比较可得哪组学生成绩更稳定;
(2)分别计算在甲、乙两组中各抽出一名同学及成绩和低于20分的取法种数,代入古典概型概率公式,可得答案.
试题解析:
(1)![]() 甲=
甲=![]() =10,
=10,
![]() 乙=
乙=![]() =10,
=10,
∴x=1,
又![]() =
=![]() [(10-9)2+(10-9)2+(11-10)2+(11-10)2]=1,
[(10-9)2+(10-9)2+(11-10)2+(11-10)2]=1,
![]() =
=![]() [(10-8)2+(10-9)2+(11-10)2+(12-10)2]=
[(10-8)2+(10-9)2+(11-10)2+(12-10)2]=![]() ,
,
∴![]() ,∴甲组成绩比乙组稳定.
,∴甲组成绩比乙组稳定.
(2)记甲组4名同学为:A1,A2,A3,A4;乙组4名同学为:B1,B2,B3,B4.分别从甲、乙两组中各抽取一名同学所有可能的结果为:(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),(A2,B2),(A2,B3),(A2,B4),(A3,B1),(A3,B2),(A3,B3),(A3,B4),(A4,B1),(A4,B2),(A4,B3),(A4,B4),共16种. 10分
其中得分之和低于20分的共6种,
∴得分之和低于20分的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣ ![]() ,an+1=
,an+1= ![]() (n∈N+)
(n∈N+)
(1)证明数列{ ![]() }是等差数列并求{an}的通项公式.
}是等差数列并求{an}的通项公式.
(2)数列{bn}满足bn= ![]() (n∈N+).求{bn}的前n项和Sn .
(n∈N+).求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
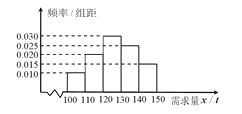
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:a1=1,an+1=3an , n∈N+ .
(1)求{an}的通项公式及前n项和Sn;
(2)已知{bn}是等差数列,Tn为前n项和,且b1=a2 , b3=a1+a2+a3 , 求T20 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为对考生的月考成绩进行分析,某地区随机抽查了![]() 名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
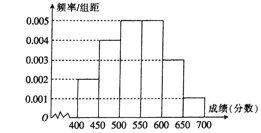
(1)求成绩在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这![]() 人中用分层抽样方法抽取出
人中用分层抽样方法抽取出![]() 人作出进一步分析,则成绩在
人作出进一步分析,则成绩在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为
为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com